我们首先尝试将Kernel用在Linear Regression,一般情况下,我们更多的考虑的是带有L2正则化的线性回归,也就是岭回归
Kernel Ridge Regression
对于L2规则化的线性模型为:
\[\min_w \ \frac{\lambda}{N}w^Tw+\frac{1}{N}\sum_{n=1}^Nerr(y_n, w^Tz_n)\]根据上文的推导,我们知道其最佳解一定为$w_* = \sum\beta_nz_n$,因此代入岭回归即可

为了求解$\beta$,我们对其求解梯度并令其为0。

那么我们显然可以得到
\[\beta = (\lambda I+K)^{-1}y\]其中$\lambda I+K$的逆显然是存在的,因为K是半正定的,且$\lambda>0$。但是其复杂度是$O(N^3)$。
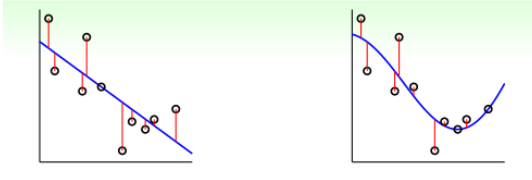
所以使用kernel可以解决非线性问题,如下左图是使用的linear ridge regression,右图使用的是kernel ridge regression。显然右图拟合更好一些。但是kernel的训练复杂度是$O(N^3)$,模型复杂度是$O(N)$,所以他一般适用于N不是很大的场合。
Support Vector Regression(SVR)
现在我们探究一下kernel ridge regression是否可以用于处理分类问题,根据前面的经验,我们给出肯定的答案,且将其应用在classification上取个新名字,叫least-squares SVM(LSSVM)。
SVR Primal
LSSVM虽然可以用在分类问题上,但是他并没有提高太多的性能,相反,他还会增加计算量。如图

因为LSSVM中$\beta$大部分是非零的,所以大部分的点都是SV,那么我们就会导致g的计算量大,降低计算速度。
为了改变LSSVM中$dense\ \beta$这一缺点,我们需要使用一些方法来得到sparse $\beta$。一个方法就是引入一个Tube Regression的做法,即在分类线上下划分一个区域,如果数据点分布在这个区域内,就不算分类错误,只有误分在中立区域之外的地方才算error。
假设中立区的宽度为$2\epsilon$, 那么error就可以写作$err(y, s)=max(0, \vert s-y\vert- \epsilon)$。通常将这个err叫做
$\epsilon\text{-insensitive error}$如图
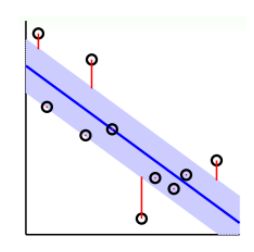
tube error与squared error其实没有太大的差别,当s接近y时,两者接近,当s远离y时,squared error的增长速率比tube error还要大的多。error增长幅度越大,表示越容易受噪声影响,不利于最优化问题的求解。所以,从这个方面看,tube regression甚至强过squared error
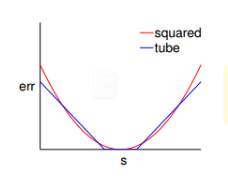
现在我们的L2-Regularized Tube Regression就出来了:
\[\min_w \ \ \ \frac{\lambda}{N}w^Tw+\frac{1}{N}\sum_{n=1}^{N}\max(0, \vert w^Tz_n-y\vert -\epsilon)\]因为里面包含了max项,不是处处可微分的,所以,我们可以考虑将其转换为的带有条件的QP问题。然后引入kernel,得到KKT条件,从而保证$\beta$是sparse的。
所以我们将其写成SVM形式:
\[\min_{b,w} \ \ \ \frac{\lambda}{N}w^Tw+C\sum_{n=1}^{N}\max(0, \vert w^Tz_n+b-y_n\vert -\epsilon)\]然后类比于SVM可以得到如下右图:

其中$\xi_n^{\bigvee}$和$\xi_n^{\bigwedge}$分别表示upper tube violations和lower tube violations。这种形式就叫做Support Vector Regression primal
\[\begin{align} \min_{b, w, \xi_n^{\bigvee}, \xi_n^{\bigwedge}} \ \ \ &\frac{1}{2}w^Tw+C\sum_{n=1}^N(\xi_n^{\bigvee}+\xi_n^{\bigwedge})\\ s.t. \ \ \ &-\epsilon-\xi_n^{\bigvee}\le y_n-w^Tz_n -b \le \epsilon+\xi_n^{\bigwedge}\\ & \xi_n^{\bigvee}\ge 0,\xi_n^{\bigwedge}\ge 0 \end{align}\]所以,SVR的QP形式一共d+1+2N个参数,2N+2N个条件。
SVR Dual
(具体推导过程,我搁这里先暂时忽略了。。)
通过SVR的primal,我们推导SVR的Dual形式。引入拉格朗日因子$\alpha^{\bigvee}$和$\alpha^{\bigwedge}$。

然后和SVM一样推导和化简,得到KKT条件

最终得到我们的SVR Dual形式

从前文已经推导出w的解
\[w = \sum_{n=1}^{N}(\alpha_n^{\bigwedge}-\alpha_n^{\bigvee})z_n\]而相应的complementary slackness为:
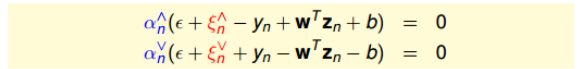
所以对于分布在tube中心区域内的点,满足$\vert w^Tz_n+b-y_n\vert<\epsilon$,此时忽略错误,$\xi_n^{\bigvee}$和$\xi_n^{\bigwedge}$都为0,那么就可以推出$\alpha_n^{\bigvee}$和$\alpha_n^{\bigwedge}$都为0。即$\beta_n = \alpha_n^{\bigwedge}-\alpha_n^{\bigvee} = 0$,即得到了sparse $\beta$。
Summar of Kernel Models
为了处理分类问题,我们引入了PLA/pocket模型,之后我们提出了linear soft-margin SVM,之后我们对模型进一步改进得到SVM的对偶形式,并引入kernel。
为了处理回归问题,从最开始的linear regression,到引入正则化提出linear ridge regression。然后我们为了解决非线性问题,我们引入了kernel ridge regression。但是他的计算量还是很大,因此提出了上文中的linear SVR,然后将其对偶化得到SVR dual形式。
为了处理逻辑回归问题,从最开始的logistic regression到regularized logistic regression再引入kernel提出kernel logistic regression处理非线性问题,但是在这一类问题中,最常用的仍然是probabilistic SVM
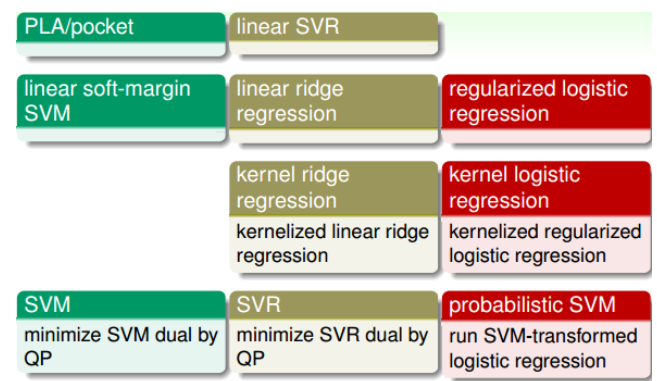
一般来讲,第一行的计算量太大,而第三行的结果又没有稀疏性,第二行和第四行的模型被使用的概率更大,其中SVR和probabilistic SVM最为常用。