Ensemeble(集成学习)
在前面的机器学习算法中,我们是在无数模型中选择最优解,尤其是交叉验证更是帮助我们进一步选择好的结果。但是如果有多个表现不好的模型将他们聚合在一起进行投票,我们仍然可以得到一个好的拟合结果,也就是三个臭皮匠顶一个诸葛亮。而这种聚集的方法也被称为集成学习。
Blending
集成学习的融合方法有以下方式, 主要是投票(Voting),线性混合(Linear Blending)等, 其数学表达式为:
-
$G(x) = sign(\sum_{t=1}^{T}1*g_t(x))$
在这种情况下,我们相当于每个模型投一票,最终将投票次数最多的设为最终结果
-
$G(x) = sign(\sum_{t=1}^{T}\alpha_tg_t(x))$
加权重的投票,这种情况可以类比到现实世界,比如做股票预测,有些人比较擅长进行股票预测,那么我们就应该更多的听从他的建议给他分配更多的权重
-
$G(x) = sign(\sum_{t=1}^{T}q_t(x)p_t(x)$
这种情况比较复杂,实际上我们的样本也是不同的,仍然以现实中股票预测为例,我们的样本中包含服务行业的股票,也包含传统行业的股票,对于不同的人他们对不同产业的认知不同,所以当我们预测服务行业的时候,就给精通服务行业的人较大权重,对预测传统行业也是这样。
上面三种聚合方式有很明显的包含关系,即上面的表达情况实际上是下面的特例。
为什么Aggregation会工作的比较好,从以下两种情况来分析。
-
情况一,如下图
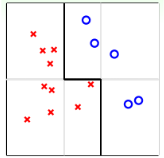
对于上面的样本,简单的线性回归其实效果并不会太好(其实还好啦,只是举例),为了更好的拟合它,按照以往的经验,我们需要进行一定的特征转换(feature transform)。
但是如果使用Aggregation,我们可以将简单的分类器拟合在一起,比如上图的分类器我们是通过简单的水平或者垂直的线进行分类,然后进行拟合,最终得到了一个比较好的结果。也就是说,Aggregation提高了预测模型的power,起到了feature transform的效果。
-
情况二,在使用PLA的时候,供我们选择的线是非常多的
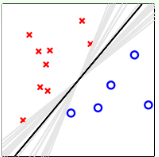
但是最理想的结果是最中间的黑线,这也是我们使用SVM的目标。但是如果我们只用Aggregation将所有的分类边界组合,我们会得到中间的那条线,这比SVM的计算要简单的多。而这种结果从实际上讲也是正则化(regularization)的效果。
综上Aggregation具有非常好的效果,他可以起到feature transform和regularization的效果。
Uniform Blending
假设我们已经有了一些性能比较好的$g_t$,然后我们将其整合合并,这个过程就被称为blending。
最简单的一种Blending是uniform blending
对于分类问题classification而言:
\[G(x) = sign(\sum_{t=1}^{T}1*g_t(x))\]然后我们选择投票数最多的为我们的最终结果。
对于回归问题Regression,我们的表达式为:
\[G(x) = \frac{1}{T}\sum_{t=1}^{T}g_t(x)\]也就是说取平均结果,从数据上看,我们去平均值的操作要比单一的$g_t$的效果要好,其推导如下:

可见$avg((g_t(x)-f(x)^2)$与$(G-f)^2$相差一个$avg((g_t-G)^2)$,所所以$g_t$与目标函数的差距比G与f的差值大。
从期望的角度来看,也可以看出G的效果比较好:
\[avg(E_{out}(g_t)) =ave(\varepsilon(g_t-G)^2)+E_{out}(G)\ge E_{out}(G)\]Linear Blending
如果使用Linear blending,我们为不同$g_t$赋予不同的权重$\alpha_t$,其中$\alpha_t>0$,那么我们最终的结果就是:
\[G(x) = sign(\sum_{t=1}^{T}\alpha_t*g_t(x))\ with \alpha_t\ge 0\]对于确定$\alpha_t$的值,实际上也是一种误差最小化的思想,即$\min\limits_\alpha E_{in}(\alpha)$。其中$E_{in}$为:
\[E_{in}(\alpha) = \frac{1}{N}\sum_{n=1}^{N}(y_n-\sum_{t=1}^{T}\alpha_tg_t(x_n))^2\]如果我们将$g_t(x)$看成一种feature transform,即:
\[\Phi(x_n) = \{g_1(x_n), g_2(x_n), g_3(x_n), g_4(x_n), ...., g_T(x_n) \}\]我们完全可以看成是一种是一种线性拟合,我们可以使用带有条件的线性回归就可以得到我们的$\alpha$。
\[E_{in}(\alpha) = \frac{1}{N}\sum_{n=1}^{N}(y_n-\sum_{t=1}^{T}\alpha_t\Phi_t(x_n))^2 \ with\ \alpha_t>0\]现在谈一下$\alpha>0$的条件,因为当我们的$g_t$越正确我们的$\alpha_t$越大,实际上如果在拟合过程中发生了使$\alpha_t<0$的情况,那显然是因为$g_t(x)$实在过于糟糕。
也就是说如果$g_t(x)$过于糟糕,比如$E_{in}(g_t)=99\%$, 错误率达到99%,而对于这种情况我们也许会得到一个$\alpha_t<0$。这实际上是对$g_t$的反向利用,即$g_t$认为是正确的,我们就认为是错误的。显然,反向的$g_t$是一个不错的结果。$\alpha_t<0 \Rightarrow \alpha_tg_t(x_t) = \vert \alpha_t\vert(-g_t(x))$
所以,实际上$\alpha_t>0$的条件是无关紧要的,我们完全可以使用线性回归来寻找我们的$\alpha$。
此外,一个更有效的改进方法是在线性拟合获得$\alpha$时,使用验证集而不是训练集。我们在获取$g_t$时一般都使用了validation。所以我们可以通过$D_{train}$来获得我们的$g^{-}(x)$,然后在训练$\alpha$的时候使用$D_{val}$,这会使我们得到一个更好的结果。
元算法
在集成学习中我们需要生成元算法,即弱分类器,然后可以将其进行混合,对此主要有两种方式:
- bagging: 元学习器之间不存在依赖关系,而是使用样本随机化来生成元学习器, 比如随机森林
- Boosting: 元学习器存在依赖关系,我们是基于前面模型的训练结果生成新的模型,比如串行化生成。比如Adaboost, GBDT等
Bagging
现在需要探讨如何获得$g_t$,一般我们有四种方式:
- 不同的模型
- 不同的参数
- 算法的随机性(eg. PLA的起点改变会得到不同的结果)
- 不同的随机数据
此外,不同的$g_t$最好是使用不同的数据集,但是实际情况中,我们往往只有一份数据集,为了从这一份数据集中模拟新数据,使用了一种方法叫bootstrapping。思想就是从已有数据集模拟出其他类似的样本$D_t$。
bootstrapping的做法就是从已有的N笔资料,先从中选出一个样本,再放回去,再选择一个样本,再放回去,重复M次后,会得到一份新的M笔资料$\check{D}_t$。我们就可以使用这份资料拟合出一个$g_t$,然后在进行aggregation。利用bootstrap进行aggregation的操作就被称为bagging。
算法过程
for t = 1….T: 1. 使用bootstrapping从原始数据获得M笔资料$D_t$ 2. 使用演算法$A(D_t)$求出$g_t$ G = aggregation(${g_t}$)
Boosting
Adaboost
使用bootstrap可以获得$g_t$,然后使用线性回归拟合获得$\alpha_t$进行合并,实际上有更加简单的方法,这种方法在获得$g_t$的同时就可以直接求得$\alpha_t$。
从Bootstrap开始说起,我们在使用Bootstrap是有放回的,也就是说我们的样本有可能被重复抽取。
假设我们有四个样本${(x_1, y_1),(x_2, y_2), (x_3, y_3), (x_4, y_4)}$。
其中一次的抽取结果为${(x_1, y_1),(x_1, y_1), (x_3, y_3), (x_4, y_4)}$。那么我们的目标函数为:
\[\min\ E_{in}(g_t) = \frac{1}{4}\sum_{n=1}^4u_nerr(y_n, g_t(x_n))\\ u_n = \{2, 0, 1, 1\}\]也就是说我们为每一个样本分配了权重,但是这实际上和原本的$E_{in}$没有任何区别,这种方法被称作Weighted Base Algorithm。
所以我们的$g_t$的求解方法如下:
\[g_t \leftarrow \mathop{\arg\min}_{h\in H}(\sum_{n=1}^{N}u_n^t[[y_n\neq h(x_n)]])\]我们该如何确定我们的$u_n$。因为在使用aggregation时,我们应当尽量是选择不同的$g_t$,$g_t$和$g_{t+1}$越不同,我们最终组合的效果会越好。因为如果大家都是同样的结果,即相同的$g_t$,实际上无论我们如何组合都只会跟$g_t$一致,就失去了聚合的意义。
因为$g_t$和$g_{t+1}$的求解方式如下:
\[g_t \leftarrow \mathop{\arg\min}_{h\in H}(\sum_{n=1}^{N}u_n^t[[y_n\neq g_t(x_n)]])\\ g_{t+1} \leftarrow \mathop{\arg\min}_{h\in H}(\sum_{n=1}^{N}u_n^{(t+1)}[[y_n\neq g_{t+1}(x_n)]])\]显然$g_t$由$u_n^t$决定,$g_{t+1}$由$u_n^{t+1}$决定,如果$g_t$和$g_{t+1}$相似,则两者在$u_n^{t+1}$上应当表现的结果是一样的,所以如果我们能够定义$u_n^{t+1}$使$g_t$在其身上表现的越差越好,则$g_t$和$g_{t+1}$就会非常不同。
一般是在$g_t$的作用下,$u_n^{t+1}$的表现(即err)近似为0.5,表明$g_t$的预测基本没什么用,就跟抛硬币一样是随机的。使用表达式为:
\[\frac{\sum_{n=1}^Nu_n^{t+1}[[y_n\neq g_t(x_n)]]}{\sum_{n=1}^Nu_n^{t+1}} = \frac{1}{2}\]为了进一步简化计算,我们定义了:

为了使分式为0.5, 我们只需要将犯错的和没有犯错的数量相等就可以了,这就是我们求解$u_n^{t+1}$的思想。
我们是已知$u_n^t$的,假设我们的$u_n^t \text{of incorrect}$为1126, $u_n^t$ of correct为6211,为了是$u_n^{t+1}$中的错误比例正好为0.5, 那么我们的做法是:
-
for incorrect $u_n^{t+1}$:
\[\sum_{n=1}^Nu_n^{t+1} = \sum_{n=1}^{N}u_n^t * 6211 \Rightarrow u_n^{t+1} = u_n^{t}*6211\] -
for correct $u_n^{t+1}$
\[\sum_{n=1}^Nu_n^{t+1} = \sum_{n=1}^{N}u_n^t * 1126 \Rightarrow u_n^{t+1} = u_n^{t}*1126\]
更流行的做法是使用犯错的比率,假设犯错误率为$\epsilon_t$,那么求解$u_n^{t+1}$的时候,$u_t^{t}$分别乘以$1-\epsilon_t$和$\epsilon_t$。
为了进一步简化,我们提出新的尺度因子: \(\Diamond t = \sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\)
对于新的尺度因子,对于错误的$u_n^t$,将它乘以$\Diamond t$, 对于正确的$u_n^t$,将它除以$\Diamond t$。这种操作与前面并没有太大的区别。因为如果$\epsilon_t<0.5$, 那么$\Diamond t>1$,错误的点乘以他,则相当于将错误的点放大,而正确的点相除则是将正确的点缩小。最终仍能得到$g_t$与$g_{t+1}$不同的结果。
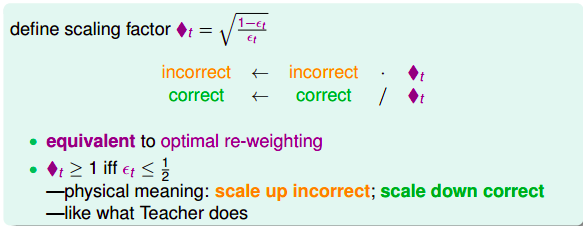
这样,我们解决了如何从$u_n^t$得到$u_n^{t+1}$的过程,如果我们只需要定义一个初始的$u_n^1$,我们就可以得到不同的$g_t$进行合并。
对于初始的$u_n^1$,我们一般定义为$u_n^1=\frac{1}{N}$,之后逐次迭代更新。
而合并我们通常是使用线性组合,他可以表现的更好,在前面,我们是通过将$g_t$看作是特征转换进行线性拟合,而Adaboost算法提供了一种更巧妙的算法可以使得每次计算$g_t$的时候同时计算出$\alpha_t$。
我们知道$\alpha_t$和错误率有很大的关系,错误越多则分配的权重越小,因为$\epsilon_t$越小,$\Diamond t$越大,所以,我们可以构造出:
\[\alpha_t = ln(\Diamond t)\]这样取值是有物理意义的,例如当$\epsilon_t=\frac12$时,error很大,此时对应的$\Diamond t=1$,$\alpha_t=0$,即此$g_t$对G没有什么贡献,权重设为零。而当$\epsilon_t=0$时,没有error,表示该$g_t$预测非常准,此时$\Diamond t=\infty$,$\alpha_t=\infty$,即$g_t$对G贡献非常大,权重应该设为无穷大。 综上我们总结出了Adaboost(Adaptive Boosting)的整个算法流程,他有三部分组成:

算法过程
最终我们的算法过程为:
需要注意的是在选择学习算法时,一般选择比较弱的学习算法,一个简单的例子就是Decision Stump,即每次只是从一个维度进行分割。简单的说就是先选择一个维度,然后随机切上一刀。
注意:
有因为对于分类正确的点有$y_ng_t(x_n)=1$, 对于分类错误的点$y_ng_t(x_n)=-1$, 而$\alpha_t = ln(\Diamond t)\leftrightarrow\Diamond t = exp(\alpha_t)$
所以我们更新$u_n^t$的时候具体的更新为:
\[\text{for incorrect:} \ \ u_n^{t+1} = {u_n^{t}*exp(\alpha_t)}\\ \text{for correct:} \ \ u_n^{t+1} = {u_n^{t}*exp(-\alpha_t)}\\\]即
\[u_n^{t+1} = {u_n^t\exp(-y_n\alpha_t g_t(x_n))}\]所以算法步骤为(计算公式同上):
u = [1\N, 1\N, …, 1/N] for t = 1, 2, 3, 4….. T
- 计算gt
- 计算错误率$\epsilon$, 然后计算$\alpha$
- 更新新的权重,$u^{t+1}$
return G(x)
理论支撑
根据前面的VC Bound角度来看,Adaboost满足:
对于这个VC Bound,其中第一项,如果满足$\epsilon_t \le \epsilon< 0.5$ , 则经过$T = O(logN)$次迭代后,$E_{in}$可以降到很低,而当N很大时,第二项也可以很小,所以$E_{out}$被限定在一个有限的上届。这正是Adaboost的精髓之处,只要我们的$g_t$比乱猜好一点点($\epsilon_t \le \epsilon< 0.5$ ),那么经过迭代后,我们会得到一个很强的G。