Validation
在机器学习的实际操作中,我们面临着许多选择,比如学习算法(PLA, 线性回归,逻辑回归等),迭代次数,学习速率,模型,正则化,正则化系数。不同的选择不同的搭配会有不同的效果,我们的目标就是找到最合适的搭配,得到我们的目标$g^*$。
一个想法是使用$E_{in}$,选择最小的$E_{in}$,但是可能发生过拟合现象。
另一个想法是使用一个测试集,然后寻找使测试集$E_{test}$最小的模型为最佳模型,但是在实际操作中,我们是得不到测试集的,因此,我们折中的想法是从训练集D中划分出一部分$D_{val}$作为验证集(validation set)。
也就是说,D中一部分用于训练模型,而另一部分用来评估模型。
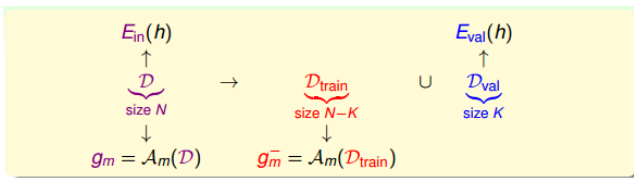
对于训练集,根据霍夫丁不等式:
\[E_{out}(g_m^-) \le E_{val}(g_m^-)+O(\sqrt \frac{logM}{K})\]根据learning curve可得,训练样本越多,得到的模型越好,我们将训练样本分离了一部分,这也导致了D的$E_{out}$要小于$D_{train}$的$E_{out}$。
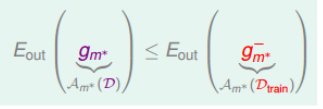
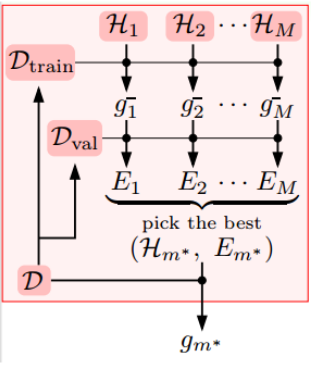
为了防止这一点,我们是先通过验证集找到较好的模型,然后重新使用全部样本再次训练。
即,假设有M个模型的hypothesis set,我们首先通过$D_{train}$来训练这M个模型,然后,我们使用$D_{val}$来评估这些模型,并从中选出一个最好的$m^*$作为我们最终的模型,然后,我们使用全部训练样本重新训练模型,得到最佳结果。
不等式关系满足:
\[E_{out}(g_{m^*}) \le E_{out}(g_{m^*}^-) \le E_{val}(g_{m^*}^-)+O(\sqrt \frac{logM}{K})\]对于验证集的数量K,一般我们会选择$\frac{N}{5}$,因为,随着K数量的增加会导致训练集减少,从而使得到的模型不具有太好的泛化能力。
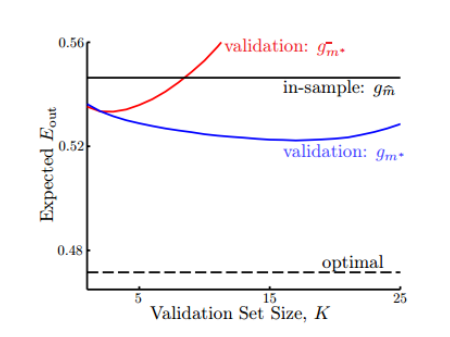
Leave-One-Out Cross Validation(留一法交叉验证)
如果我们的验证集大小为1,即每次只是用一组数据进对$g_m$进行验证,这样的优点是$g_m ^- \approx g_m$。但是$E_{val}$和$E_{out}$可能相差很多。因此,我们提出一种留一法交叉验证。
留一法交叉验证中,我们的验证集数量只有1,但是我们将所有的样本都当做一次验证集,即,对于一个模型,我们一共计算N次,最后最验证误差求平均,得到$E_{loovc}(H, A)$。
\[E_{loocv}(H, A) = \frac{1}{N}\sum^N_{n=1}e_n = \frac{1}{N}\sum^N_{n=1}err(g_n^-(x_n), y_n)\]一个具体的例子如下:
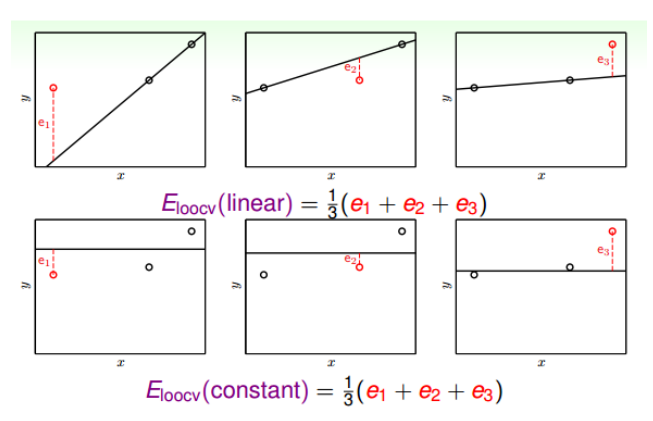
计算err的时候,我们使用验证集的模型是由剩下N-1个训练集得到的,也就是说,模型训练也要进行N次。得到的N个g,然后分别与对应的验证集进行计算,最终得到一个平均值。
然后选择一个值比较小的作为最终结果。
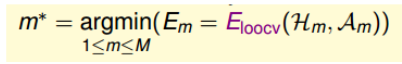
从理论上将,假设有不同的训练集D,他们的期望分布为$\varepsilon_D$,则其$E_{loocv}(H, A)$可以通过推到,等于$E_{out}(N-1)$的平均值。由于N-1近似N,$E_{out}(N-1)$的平均值也近似等于$E_{out}(N)$。具体推导如下(我是推不出来了。。):
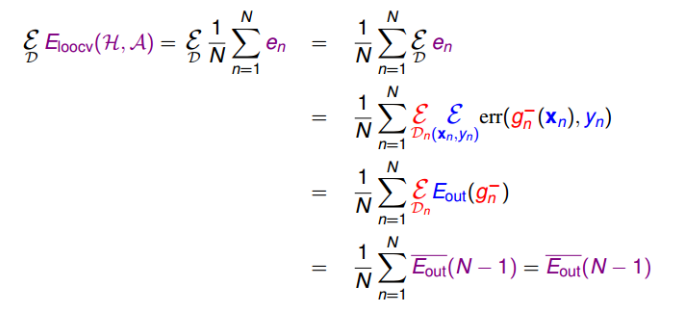
V-Fold Cross Validation
对于留一法交叉验证,如果N过大,那么计算量会非常大,因此,一个改进的方法,是将N个数据分为V份,然后计算思路与留一法交叉验证相似,这样可以减少总的计算量,又能得到好的g,这种方法称为V-折交叉验证。在实际中,通常使用这种方法。
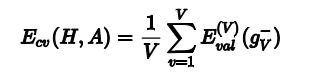
值得一提的是,Validation的数据来源也是样本集中的,所以并不能保证交叉验证的效果好,他的模型就一定好,只有样本数据越多,越广泛,那么Validation越可信,其选择的模型的泛化能力越强。
总结
以逻辑回归为例,我们有步长$\eta$, 还有训练的权重$w$, 而我们的$\eta$不是训练出来的,而是人为选择的,所以,不同的步长就代表着不同的模型。
我们首先选定一个超参数,形成一个模型,然后对其进行交叉验证,得到一个$E_{cv}$, 这个就是我们对这一模型的评估效果。
其算法过程:
- 随机将训练数据分为k份,D1, D2, …Dk;
- 选定一个超参数即得到一个模型, 然后对这个模型进行交叉验证,得到一个误差$E_{cv}$。
- 重复进行第二步,找到一个$E_{cv}$最小的模型作为最终模型, 也就是超参数作为最终超参数。然后在整个训练集上重新训练该模型,得到最终的模型。
Three Learning Principles
- Occam’s Razor: 选择时,应尽量从简单的模型开始
- Sampling Bias: 样本采样是要广泛,在机器学习中就是训练数据和验证数据要服从同一个分布,最好是独立同分布。
- Data Snooping: 避免数据偷窥,最简单的例子就是不要拿验证数据来训练样本