Quadratic Hypothesis(二次假设)
在前文中,我们都是使用的是线性模型,但是在真实世界中,仍然存在非线性数据

对于这种数据,显然不是线性可分的,我们无法得到一个$E_{in}$足够小的直线。但是这种问题可以是圆形可分的,即圆内部为正,外部为负,则假设(hypothesis)为:
\[h_{SEP}(x) = sign(-x_1^2-x_2^2+0.6)\]对于这个假设,如果我们把$x_1^2和x_2^2$看作特征的话,那么他仍然可以被看作一个线性模型,即$w=[0.6, -1, -1]$, 而特征为$(1, x_1^2, x_2^2)$。
这就提供了一种思路,我们可以将原始特征就是组合变换,将原始空间中的点,映射到一个新的空间,比如,如果我们设置一个新的特征集合z,那么对于上述情况,显然有$z= (1, x_1^2, x_2^2)$。我们吧$x_n \rightarrow z_n$的过程称之为特征转换(feature transform)。

目前讨论的圆形是圆心过原点的,如果圆心不过原点,则$x_n \rightarrow z_n$中的映射公式包含的所有项应为:
\[\Phi(x) = (1, x_1, x_2, x_1^2, x_2^2, x_1x_2)\]Price of Nonlinear Transform(非线性转换的代价)
如果特征维度的d维的,那么如果要转换为二次多项式,那么z域维度是;
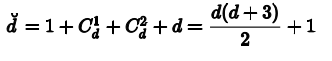
如果阶数更高,那么z域特征维度为:
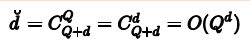
显然,这种特征变换的一个代价就是计算的时间、空间复杂度会变得极大。
另一方面,z域中特征个数随着Q和d增加变得很大,同时权重w也会增大,即自由度增加,$d_{vc}$增加。那么就会导致模型的泛化能力比较差。
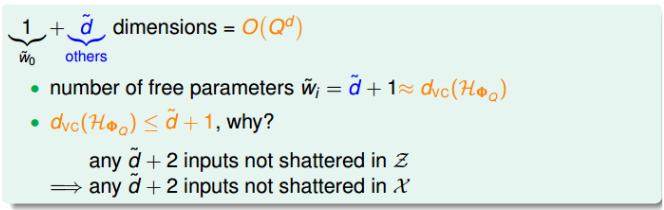
而且,过多的项数会带来过拟合的问题。

Structured Hypothesis Sets
所以我们要选择适当的Q来保证我们的模型尽可能的好。
对于从x域到z域的多项式变换,我们会得到以下的规则
如果特征维度只有一维,多项式仅包含常数项
\[\Phi_0(x) = (1)\]如果是两维,变换多项式包含了一维的$\Phi_1(x) = (\Phi_0(x), x_1, x_2, ….x_d)$
以此类推可得
如果特征维度是Q次,那么他的变换多项式为
\[\Phi_Q(x) = (\Phi_{Q-1}(x), x_1^Q, x_1^{Q-1}x_2, ...., x_d^q)\]对于不同阶次构成的hypothesis有如下关系
\[H_{\Phi_0} \subset H_{\Phi_1} \subset H_{\Phi_2} ... \subset H_{\Phi_Q}\]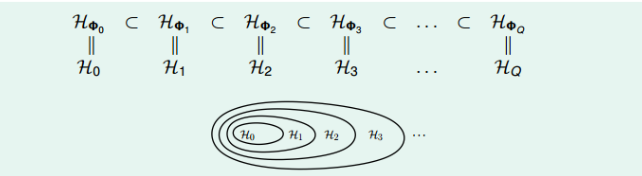
这种结构被称为Structured Hypothesis Sets。
显然,对于这种Structured Hypothesis Sets。它们的VC Dimension满足:
\[d_{vc}(H_0) \le d_{vc}(H_1) \le d_{vc}(H_2) ....\le d_{vc}(H_Q)\]他们的$E_{in}$满足:
\[E_{in}(g_0) \ge E_{in}(g_1) \ge E_{in}(g_2) \ge ... E_{in}(g_Q)\]根据前面Error与$d_{vc}$的图形:
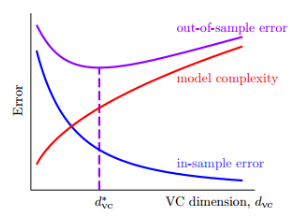
我们可知,并不是阶数越大,我们的学习效果就越好,因为当阶数过大时,尽管$E_{in}$接近于零,但是泛化能力会很差,通常情况叫这种情况为temping sin。所以,一般都是先从低阶开始,然后逐渐增加阶数,直到满足要求为止。