- Soft-Margin SVM as Regularized Model
- SVM versus Logistic Regression
- SVM for Soft binary Classification
- Kernel Logistic Regression(KLR)
- 参考
SVM除了可以用来处理二分类问题,同时他还可以进行处理逻辑回归问题,因为他与逻辑回归(Logistic Regression)是相似的。
Soft-Margin SVM as Regularized Model
soft-margin-SVM的最终目标为是
\[\begin{align} \min_{b, w, \xi}\ & \frac{1}{2}w^Tw+C\sum_{n=1}^N\xi_n\\ s.t.\ &y_n(w^Tz_n+b)\ge 1-\xi_n, \xi_n\ge 0 \end{align}\]因为$\xi$是用来描述一个点是否正确的,如果一个点不满足$y_n(w^Tz_n+b)\ge 1$。这种情况就是violating margin,则$\xi$可以表示为$\xi_n = 1-y_n(w^Tz_n+b)> 0$。第二种情况是not violating margin,即点在边界之外,这些点都是分类正确的,此时则有$\xi_n=0$。所以,我们的$\xi_n$可以表示为:
\[\xi_n = \max(1-y_n(w^Tz_n+b), 0)\]我们的Soft-Margin SVM就表示成了:
\[\min_{b, w, \xi}\ \frac{1}{2}w^Tw+C\sum_{n=1}^N\max(1-y_n(w^Tz_n+b), 0)\]这个形式就可以发现与L2 Regularization中的最优化表达式是类似的。
\[\begin{align} SVM:\ & min \frac{1}{2}w^Tw+C\sum err^{'}\\ L2: \ & min \frac{\lambda}{N}w^Tw+\frac{1}{N}\sum err \end{align}\]两着除了err的表达式不同,基本上是类似的,但是需要注意的是,经过转换的SVM是不可以通过梯度下降的方法来求解的,因为max导致了函数并不是处处可导。
在前文,我们知道了Hard-Margin SVM和正则化的类似,现在,我们又可以看到了这种类似。
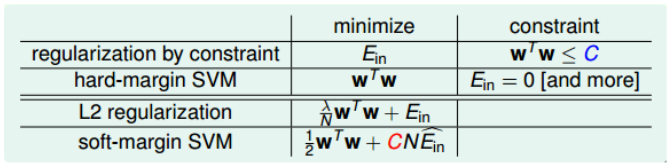
从图中可以看出,L2中的$\lambda$和SVM中的C都起到了防止过拟合的效果,只是一个是减少$\lambda$,一个是增大C。
SVM versus Logistic Regression
那么从理论上SVM是否支持机器学习算法的一大条件,即$E_{out}\approx E_{in}$。
我们类比于分析分析逻辑回归处理分类问题那样。
对于$err_{0/1}$和$err_{svm}$和$err_{sce}$三者的err曲线如图

可以看出来,$err_{svm}$和$err_{sce}$类似都是$err_{0/1}$。所以svm是可以处理分类问题的,同时,因为当ys接近无限大,$err_{svm}$和$err_{sce}$都接近于0; 当ys趋向负无限大,两者都趋向于正无穷大,所以,可以通过这种相似性,将SVM类比为L2-Regularized logistic regression。
SVM for Soft binary Classification
那么如何将SVM的结果用于处理Soft Binary Classification问题,即得到是正类的概率值。
先考虑两种简单的方法。
第一种是首先解的SVM的$(b_{svm}, w_{svm})$,然后代入logistic regression中,得到g(x),这种情况直接使用了SVM和LR的相似性,一般表现不错,但是过于简单,与LR关联不大,没有使用LR中好的性质和方法。
第二种是首先解SVM的$(b_{svm}, w_{svm})$,然后将它作为LR的初始值,再进行迭代修正,速度较快,但是这种做法显得多次一举,没有比直接使用LR快捷多少。
为了融合两种方法去,我们构造了一个新的模型$g(x)$的表达式:
\[g(x) = \theta(A*(w^T_{svm}\Phi(x)+b_{svm})+B)\]即额外增加了防缩因子A和平移因子B。首先使用SVM的$(w_{svm}, b_{svm})$来构造这个模型,然后再通过LR优化算法得到最终的A和B。一般而言,如果SVM的结果较好,那么A>0且$B\approx 0$。
所以,最终我们新的逻辑回归表达式为:

虽然表达式复杂了,但是求解过程并没有特别麻烦,probabilistic SVM主要步骤是:
- 使用SVM求解$(w_{svm}, b_{svm})$和$z^{‘}n = w^T{svm}\Phi(x_n)+b_{svm}$。
- 使用LR优化算法通过$(z^{‘}n, y_n){n=1}^N$来得到(A, B)
- 返回最终结果$g(x) = \theta(A*(w^T_{svm}\Phi(x)+b_{svm})+B)$
Kernel Logistic Regression(KLR)
前面除了证实了SVM可以用于处理逻辑回归问题,实际上还有一个重要的作用,当我们进行z域转换时,我们使用SVM计算w和b会大大减少计算量,因为在SVM中我们使用了Kernel。
那么在LR中,我们可不可以直接使用Kernel trick,因为Kenel trick的形式为:$w^Tx=\sum\beta_nz_n^Tz = \sum\beta_nK(x_n, x)$
如果我们能够将LR中w转换为$w_{LR} = \sum(\alpha_ny_n)z_n$,那么显然,我们也是可以直接使用Kernel的。
事实上,的确存在这样的理论,对于L2-Regularized linear model。如果他的最小化问题形式如:
\[\min_{w}\ \frac{\lambda}{N}w^Tw+\frac{1}{N}\sum_{n=1}^{N}err(y_n, w^Tz_n)\]那么他的最优解就是$w^T_{*} = \sum\beta_nz_n$
对于这一点,我们可以通过反证法证明,证明过程如下:
我们将最有解分解为$w_{*}=w_{\Vert}+w_{\perp}$, 其中$w_{\Vert}$是位于$z_n$展开的空间平面,而$w_{\perp}$则是垂直于$z_n$展开的空间平面。
第一步: 那么显然我们可以得到$err(y_n, w^T_{*}z_n) = err(y_n, (w_{\Vert}+w_{\perp})^Tz_n)=err(y_n, w^T_{\Vert}z_n)$。对于第二项是相等的。
| 第二步: 但是对于第一项$w_^Tw_=w_{ | }^Tw_{ | }+2w_{ | }^Tw_{\bot}+w_{\bot}^Tw_{\bot}>w_{ | }^Tw_{ | }$,所以$w_*$不是最优解,从而证明$w_{\perp}$一定为0.即w可以写成z的线性组合$w = \sum\beta_nz_n$ |
因此,我们保证了可以使用Kernel来简化LR。将其带入L2-Regularized LR为:

然后我们就可以使用SGD或者GD来求解$\beta$。