其次,如果,我们换一个角度来看待这个公式,即将$g_t(x_n)$看成对$x_n$的特征转换$\phi_i(x_n)$,将$\alpha_t$看作线性
Adaboost的损失函数
我们知道,在adaboost中,我们的最终目标如下,
\[G(x) = sign(\sum_{t=1}^T\alpha_tg_t(x_n))\]如果我们换一个角度来看待这个公式,将$g_t(x_n)$看成对$x_n$的特征转换$\phi_i(x_n)$,将$\alpha_t$看作线性权重$w_i$。
显然,我们的$G(x) = sign(w^T\phi(x))$。此外,令$s = w^T\phi(x)$, 那么实际上,他就像是线性回归用于分类问题。我们分析一下他的损失函数。
在Adaboost中,如果使用二元分类误差,我们的损失函数为:
\[err_{0/1}(y, s) = \vert sign(s)\neq y\vert = \vert G(x_n)\neq y_n\vert\]对于这个误差,我们有一个上届,这个上届就是:$err_{ada}(y, s) = exp(-ys)$
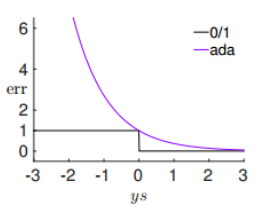
所以adaboost的损失函数可以表示为:
\[E_{in}(x) =\frac{1}{N}\sum_{n=1}^Nerr_{ada}(y, s) =\frac{1}{N}\sum_{n=1}^Nexp(-ys)= \frac{1}{N}\sum_{n=1}^N\exp(-y_n\sum_{t=1}^T\alpha_tg_t(x_n))\]我们的目标就是最小化$E_{in}$。
前向分步算法
假设加法模型为
\[f(x) =\sum_{t=1}^{T}\beta_t b(x; \gamma_t))\]其中$b(x; \gamma)$就是基函数, $\gamma$就是基函数的参数,$\beta$就是基函数的系数。
在给定训练数据及损失函数$err(y, f(x))$的条件下,学习加法模型成为经验风险最小化即损失函数最小化:
\[\min_{\beta, \gamma}\sum_{n=1}^Nerr(y_n, \sum_{t=1}^{T}\beta_t b(x; \gamma_t))\]前向分步算法是求解上述优化问题的重要方法,他的思想是,由于学习的是加法模型,如果能够从前向后,每一步只学习一个基函数极其系数,逐步优化逼近目标函数,那么就可以简化优化的复杂度。具体的就是每一步只需要优化:
\[\min_{\beta, \gamma}\sum_{n=1}^Nerr(y_n, \beta b(x_n;\gamma))\]所以我们的前向分步算法就是:
-
初始化$s_0 = 0$
-
对t=1, 2, 3, 4…., T
-
极小化损失函数
\[(\beta_t, \gamma_t) = \mathop{argmin}_{\beta, \gamma}\sum_{n=1}^{N}(y_n, f_{t-1}(x_n)+\beta b(x_n; \gamma))\] -
更新:
$f_t(x) = f_{t-1}(x) +\beta_t b(x; \gamma_t)$
-
-
得到加法模型:
\[f(x) = \sum_{t=1}^{T}\beta_t b(x; \gamma_t)\]
他其实与我们的adaboost是极其相似的,在adaboost中,我们的基函数就是$g_t(x)$, 其系数$\beta$就是$\alpha_t$, $\gamma$就是$u_t$。而我们的$E_{in} = \frac{1}{N}\sum_{n=1}^Nerr_{ada}(y, s)$.
Adaboost与前向分步算法
在adaboost中,我们的最终目标是:
\[f(x) = \sum_{t+1}^T\alpha_tg_t(x)\]而我们的最小化目标函数是:
\[E_{in}(x) =\frac{1}{N}\sum_{n=1}^Nerr_{ada}(y, f(x)) = \frac{1}{N}\sum_{n=1}^N\exp(-y_nf(x_n))\]我们完全可以用前向分步算法来解决这个问题。
其中,假设经过t-1轮后得到$f_{t-1}(x)$为:
\[\begin{align} f_{t-1}(x) = &f_{t-2}(x) + \alpha_{t-1}g_{t-1}(x)\\ = & \alpha_1g_1(x)+\alpha_2g_2(x) + .. +\alpha_{m-1}g_{m-1}(x) \end{align}\]所以在第t轮迭代中得到$\alpha_t, g_t(x)$和$f_t(x)$。
\[f_t(x) = f_{t-1}(x)+\alpha_tg_t(x)\]而我们求解$\alpha_t, g_t(x)$的方法就是:
\[(\alpha_t, g_t(x)) = \mathop{argmin}_{\alpha, g}\frac{1}{N}\sum_{n=1}^N\exp[-y_n( f_{t-1}(x)+\alpha g(x))]\]我们令:
\[\begin{align} u_n^{T}& =u_n^{t-1}exp(-y_n\alpha_ng_t(x_n))\\ & = u_n^1\prod_{t=1}^{T-1}\exp(-y_n\alpha_ng_t(x_n))\\ &=\frac{1}{N}\exp(-y_n\sum_{t=1}^{T-1}\alpha_tg_t(x_n))\\ &=\frac{1}{N}\exp(-y_nf_{t-1}(x_n)) \end{align}\]所以,我们求解$\alpha_t$和$g_t(x)$的方法可以进一步简化为:
\[(\alpha_t, g_t(x)) = \mathop{argmin}_{\alpha, g}\sum_{n=1}^Nu^t_n\exp(-y_n\alpha g(x))\]为了求解这个$\alpha_t$和$g_t(x)$, 我们第一步首先忽略$\alpha$,先求解g(x), 这是因为对一切$\alpha>0$(可以令$\alpha>0$是因为,如果$\alpha<0$, 那么g(x)=-g(x)也可以), 他对g(x)是没有影响的。所以,我们的目标就是:
\[g_t(x) = \mathop{argmin}_{g}\sum_{n=1}^{N}u_n^t\exp(-y_ng(x_n))=\mathop{argmin}_{g}\sum_{n=1}^{N}u_n^terr(y_n, g(x_n))\]显然,$g(x)$就是Adaboost算法中基本分类器$g_t(x)$,比如Decision Stump,因为他是使第t轮加权训练数据分类误差最小的基本分类器。
然后我们再求解$\alpha_t$。
\[\begin{align} \sum_{n=1}^Nu^t_n\exp(-y_n\alpha g(x)) =& \sum_{y_n=g_t(x_n)}u_n^t\exp(-\alpha)+ \sum_{y_n\neq g_t(x_n)}u_n^t\exp(\alpha)\\ &=(\exp(\alpha)-\exp(-\alpha))\sum_{n=1}^Nu^t_n\vert y_n\neq g(x_n)\vert +\exp(-\alpha)\sum_{n=1}^Nu_n^t \end{align}\]我们将$g_t(x)$代入,并为其求导,暂且令$\sum_{n=1}^Nu^t_n\vert y_n\neq g(x_n)\vert=\beta$, $\sum_{n=1}^Nu_n^t=\gamma$
则:
\[\begin{align} & (\exp(\alpha)+\exp(-\alpha))\beta-\exp(-\alpha)\gamma = 0\\ \Leftrightarrow & \frac{\exp(\alpha)+\exp(-\alpha)}{\exp(-\alpha)} = \frac{\gamma}{\beta}\\ \Leftrightarrow & \alpha = \frac{1}{2}\ln(\frac{\gamma}{\beta}-1) \end{align}\]因为
\[\epsilon = \frac{\sum_{n=1}^Nu^t_n\vert y_n\neq g(x_n)\vert}{\sum_{n=1}^Nu_n^t}\]所以得到:
\[\alpha_t = \ln(\sqrt\frac{1-\epsilon}{\epsilon})\]可知$\alpha_t$也是在adaboost中求解的$\alpha_t$。
综上所述,我们使用前向分步求解adaboost的过程与我们在前文中描述的是一致的。
GBDT
前文中使用了加法模型和前向分步算法和基函数的这种方法就被称作Gradient Boosting。而当我们使用决策树为基函数的时候就是GBDT,即Gradient Boosting Decision Tree。
所以Adaboost中使用Decision Stump是GBDT的一个特例,或者说用于处理分类问题的一种方法,而GBDT不仅可以处理分类问题,同时他也可以处理回归问题。我们以CART决策树为基函数:即
\[G(x) = \sum_{t=1}^TT(x; \Theta_t)\]所以我们的目标就是:
\[\Theta_t= \mathop{argmin}_{\Theta}\sum_{n=1}^{N}err(y_n, f_{t-1}(x_n)+T(x_n;\Theta))\]在处理回归问题中, 我们的err为$err(y, f(x)) = (y-f(x))^2$, 所以在此处,我们的损失为:
\[\begin{align} err(y, f_{t-1}(x)+T(x;\Theta)) =& [y-f_{t-1}(x)-T(x; \Theta)]^2\\ =&[r-T(x; \Theta)]^2 \end{align}\]其中$r =y-f_{t-1}(x) $, 就是当前模型的残差(residual)。所以,其实在GBDT中,我们只需要简单的拟合当前模型的残差即可.
算法流程:
-
初始化$f_0(x)=0$
-
对t=1, 2, … T。
-
计算残差r
$r_t = y-f_{t-1}(x)$
-
拟合残差$r_t$, 通过CART学习一个回归树$T(x; \Theta_t)$
-
更新$f_m(x) = f_{m-1}(x)+T(x;\Theta_t)$
-
-
得到回归问题GBDT
\[f_T(x) = \sum_{t=1}^TT(x; \Theta_t)\]
参考
[统计学习方法]