机器学习(13)-决策树

• 决策树
  • ID3和C4.5
    • 特征选择
      • ID3
      • C4.5
    • 决策树生成算法
    • 剪枝
  • CART(classification and regression tree)
    • 回归树
    • 分类树
    • 剪枝
• 参考

决策树(Decision Tree)也是一种aggregation方法，他是一种基于条件(conditional)的aggregation。

决策树跟人的思维方式十分相似，我们会对逐个条件进行判断然后最终得到我们的结果,如图

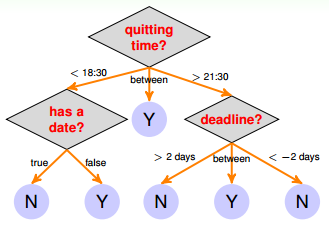
图中每个条件和选择都决定了最终的结果。其中蓝色的表示为叶子就是最终的决定。

首先他的数学表达是为:

其中$g_t(x)$是常数，也就是要么为+1,要么为-1。把$g_t$称为base hypothesis。$q_t(x)$表示$g_t(x)$成立的条件，也就是途中的路径，不同的$g_t(x)$对应不同的$q_t(x)$。

除了这种表示方法之外，更普遍的是使用条件分支的思想，将整棵树分为若干子树， 将G(x)分为若干$G_c(x)$:

其中G(x)为整个树，$G_c(x)$为子树，而b(x)为分支条件。

决策树有他的优点和缺点:

决策树

决策树的目标是:

因此，我们可以简单的总结出决策树的算法过程。

首先确定划定分支的标准和条件;之后将数据集D根据分支个数C和条件划分为不同的子集$D_c$；然后递归训练不同的子树$G_c$；最后将他们组合在一起形成G(x)。需要注意的是，我们必须要有终止条件，否则程序会一直进行下去，当满足终止条件时，返回基本的hypothesis $g_t(x)$。

所以综上所述，决策树的基本演算法包括四个部分:

• 分支个数
• 分支条件
• 终止条件
• 基本算法

我们可以将分支条件和分支个数看成特征选择，将基本算法和终止条件当作决策树的生成，最后为了防止过拟合，我们增加了决策树的剪枝。

现在我们就从这几个方面来介绍决策树算法:

ID3和C4.5

构建决策树的方法大致有三种，分别是ID3，C4.5和CART。我们将大致介绍一下前两种算法。而将主要注意力放在CART。

ID3和C4.5仅适用于分类问题，对于ID3仅适用于离散性特征，而C4.5可以使用连续性特征

特征选择

ID3

信息增益由经验熵和条件熵组成。举一个简单的例子:

假设训练集为D，$\vert D\vert$是其样本数量。设有K个类$C_k$，其中$\vert C_k \vert$就是属于$C_k$类的样本个数。设特征A有n个不同的取值(例如年龄可以分为青年，中年，老年)。根据特特征A的n个取值将训练集D分为n个子集$D_1, D_2,,,,D_n$。并且记$D_{ik}$为自己$D_i$中属于$C_k$类的样本集合。那么信息增益算法为:

1. 计算数据集D的经验熵

   \[H(D) = -\sum_{k=1}^K\frac{\vert C_k\vert}{\vert D \vert}\log_2\frac{\vert C_k\vert}{\vert D\vert}\]

2. 计算特征A对数据集D的经验条件熵:

   \[H(D\vert A) = \sum_{i=1}^{n}\frac{\vert D_i\vert}{\vert D\vert}H(D_i) =-\sum_{i=1}^{n}\frac{\vert D_i\vert}{\vert D\vert}\sum_{k=1}^K\frac{\vert C_{ik}\vert}{\vert D_i \vert}\log_2\frac{\vert C_{ik}\vert}{\vert D_i\vert}\]

3. 计算信息增益

   \[g(D, A) = H(D) - H(D\vert A)\]

C4.5

ID3更倾向于取值比较多的特征，所以为了改进他，提出了C4.5的概念。与ID3不同的是，C4.5可以处理连续性数据，但是仍然只能处理分类问题。他使用了一种信息增益比的概念。也就是说是其信息增益与训练数据关于特征值A的熵$H_A(D)$之比。

决策树生成算法

输入: 训练样本集D，特征集A，阈值$\varepsilon$

1. 若D中所有实例都属于同一类$C_k$，则T为单节点树，并将$C_k$作为该节点的类标记，返回T;
2. 若A=$\Phi$，则T为单节点树，并将D中实例数最大的类$C_k$作为该节点的标记，返回T;
3. 否则，根据ID3或C4.5选择最佳特征$A_g$
4. 判断选择特征$A_g$的信息增益或者信息增益比是否小雨$\varepsilon$，如果小于，将D中实例数最多的类$C_k$作为对该节点的类标记，返回T
5. 否则对特征$A_g$ 的每一个可能值$a_i$，将D分割为若干个非空子集$D_i$。使用数据集$D_i$构建子节点，由节点及其子节点构成树T，返回T;
6. 对第i个子节点，以$D_i$作为训练集，以$A-{A_g}$为特征集，递归调用1-5。得到子树$T_i$，返回T

剪枝

决策树生成算法递归的构建决策树，直到不能继续下去为止，虽然在生成时，我们设定了一定了终止条件，比如$\varepsilon$，但是仍然存在过拟合的风险，所以我们选择正则化（依旧不过深的探讨理论），我们的目标就变为了:

其中$E_{in}$是我们的损失函数。

在ID3和C4.5中，我们将他定义为:

其中T是树，$\vert T \vert$是树的叶子节点数，t是T的叶子节点,该叶子节点有$N_t$个样本，其中K类的样本为$N_{tk}$个，$H_t(T)$是叶子节点t的经验熵

其算法为:

1. 计算每个节点的经验熵
2. 递归的从树的叶子节点往上回缩，回缩之前树为$T_b$，回缩之后树为$T_a$，如果$E_{in}(T_a)\le E_{in}(T_b)$，那么则进行剪枝。
3. 返回2,直到不能继续为止。

CART(classification and regression tree)

CART相比于ID3和C4.5有巨大的进步，首先CART规定决策树是二叉树，并且他使用不纯度(impurity)(实际上就是误差或者错误率)的概念来选择的特征和分支。

而对于分支，如果是连续性数据，我们就选择一个切分点s，对于$x_i<s$的作为一个分支，对于$x_i\ge s$的作为一个分支;如果是离散性数据，那么就将其分为两个集合。每个集合作为一个分支。

回归树

对于回归问题，我们的不纯度就是平方误差

所以对于回归问题，我们的分支条件就是

然后选择$\mathop{argimin}_{j, s} s(x)$， 其中j是特征， s是切分点

所以其算法过程为:

输入: 训练集D, 停止条件如阈值$\varepsilon$ :

1. 输入: 训练集D, 停止计算的条件， 如$\varepsilon$
   1. 对训练集中每一个特征A，及A可能取的值a，将其分割为$D_1$和$D_2$，计算s(x)。
   2. 对遍历所有的特征和他们所有可能的取值，选择s(x)最小的作为最佳特征和最佳切分点。然后将训练数据分到两个子节点去
   3. 对两个子节点递归调用(1), (2)。直到满足停止条件
   4. 生成CART决策树。

分类树

对于分类问题，他的不纯度就是;

上述中，我们分类将样本中类别最多的样本作为我们的最终分类类别，然后判断他的不纯度。事实上，我们进一步修改了这个不纯度的计算方法:

其中，K是类别数，$\vert C_k\vert$是第k类样本的， 上述这个公式被称为基尼指数,而分类树的分支就是由基尼指数决定。

其算法过程为:

输入: 训练集D, 停止计算的条件， 如$\varepsilon$

1. 对训练集中每一个特征A，及A可能取的值a，将其分割为$D_1$和$D_2$，计算基尼指数Gini(D, A)。
2. 对遍历所有的特征和他们所有可能的取值，选择基尼指数最小的作为最佳特征和最佳切分点。然后将训练数据分到两个子节点去
3. 对两个子节点递归调用(1), (2)。直到满足停止条件
4. 生成CART决策树。

剪枝

上文中的ID3和C4.5的剪枝是可以使用的，但是我们还有更加准确复杂的剪枝方法，在此处就不做过多了解了。

参考

机器学习技法-coursera

统计学习方法[李航]