过拟合(Overfitting)
机器学习满足两个条件,即:1、$E_{in}\approx E_{out}$, 2、$E_{in}\approx 0$
对于第一个条件,他与VC Dimension有关,如果$d_{vc}$越大,那么模型的复杂度就会越高。而在前面,我们讲了非线性问题的转化,随着阶数增多,$E_{in}$会越来越小,但是$d_{vc}$也会变大,我们将$E_{in]$足够小,但是$E_{out}$足够大的问题称为bad generation,即泛化能力差。
从VC曲线的角度上看:
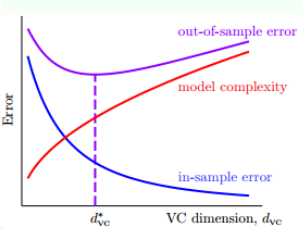
随着VC Dimension的增大,$E_{in}$越来越小,而$E_{out}$越来越大,尤其是在$d^_{vc}$的右侧,这种情况称之为过拟合(overfitting)。而在$d^{vc}$左侧,则随着VC Dimension越来越小,而$E{in}$和$E_{out}$越来越大。这种情况称为欠拟合(underfitting)。
对于overfitting和bad generation的关系。可以认为:overfitting是$d_{vc}$过大的过程,而bad generation是overfitting的结果。
一般而言,影响过拟合的原因有三种:VC Dimension、noise和样本数量N。
The Role of Noise and Data Size
现在存在两个训练样本,一个是由十阶多项式和noise构成,如图左,一个是仅仅有50阶多项式构成,如图右。
我们分别用十阶多项式和二阶多项式拟合样本一,用50阶多项式和二阶多项式来拟合样本二。
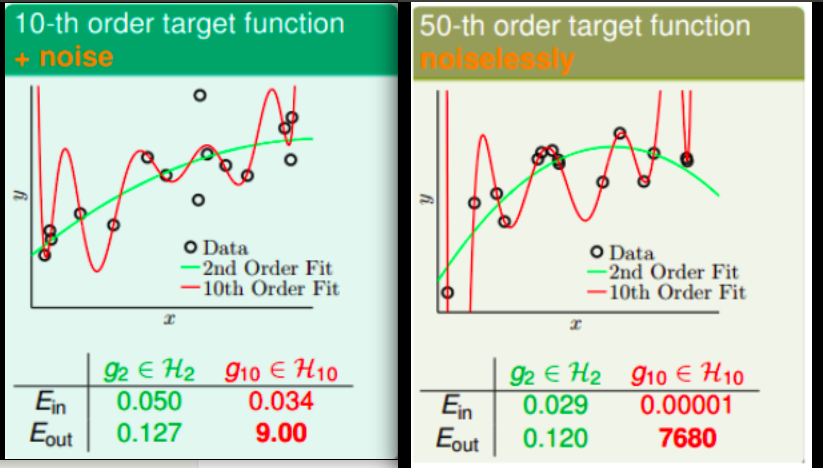
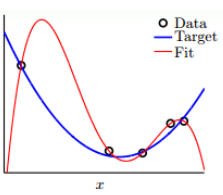
上面图一可以看出,十阶模型出现了过拟合,而二阶模型反而表现的不错。这种情况其实是机器学习中的一个原则,即,简单的学习模型反而能表现的更好。
如果使用learning curve来查看
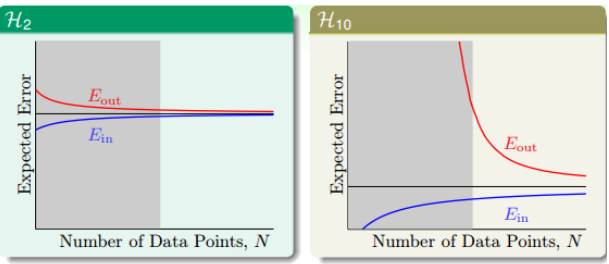
可以看到,左侧灰色部分,对于二阶多项式$E_{in}$和$E_{out}$是接近的,但是对于十阶多项式其差别极大。尽管随着样本数量的增加,十阶多项式似乎表现的不错,但是这容易发生维度灾难。
而另一个例子尽管没有噪声,但是这种复杂度本身就会引入一种噪声,这种噪声,我们称之为Deterministic Noise。
通过分析不同的$(N, \sigma^2)$和$(N, Q_f)$的关系,下图中红色越深,overfit程度越高,蓝色越深,overfit程度越低。
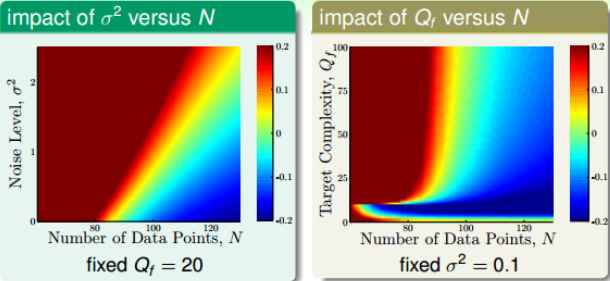
对于第一个图,可见,当$Q_f$固定后,横坐标表示样本数量N,纵坐标表示噪声水平$\sigma^2$。红色区域集中在N很小或者$\sigma^2$很大的时候,即N很大,$\sigma^2$越小,越不容易发生overfit。对右图,横坐标表示样本数量N,纵坐标表示目标函数阶数N,红色区域在N很小或者$Q_f$很大的地方。也就是说,N越小,$Q_f$越小,越不容易发生overfit。
可见,$\sigma^2$对overfit是有很大的影响的,这种noise称为stochastic noise。同样的$Q_f$对overfit也有影响,且两者相似,所以可以将这种称为deterministic noise。
因此影响overfitting的有四个因素:
- data size N $\downarrow$
- stochastic noise $\sigma^2$ $\uparrow$
- deterministic noise $Q_f$ $\uparrow$
- excessive power $\uparrow$
Dealing with Overfitting
处理过拟合的方法主要有:
- start from simple model
- data cleaning/pruning
- data hinting
- reguarization
- validataion
data cleaning/pruning就是对训练样本中label明显错误的样本进行修正(data cleaning),或者将错误的样本看成噪声进行剔除(data pruning)。
data hinting是针对N不够大的情况,如果没有办法获得更多的训练集,那么data hinting就可以对已知的样本进行简单的处理、变换、从而获得更多的样本。
Regularization
应对过拟合的一种重要方法就是使用规则化(Regularization)。
过拟合的一大问题就是因为阶数过高的原因,因此问题就变成了把高阶的hypothesis sets转换为低阶的hypothesis sets。在前文我们知道,hypothesis存在的包含关系为:
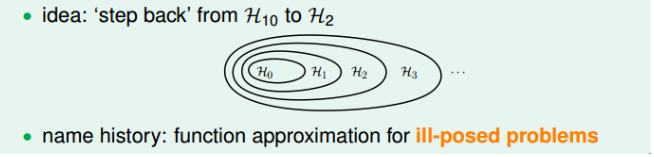
因为10阶多项式中包含了二阶多项式hypothesis sets中的所有项。即H10可以表示为:
\[H_{10} = w_0+w_1x+w_2x^2+w_3x^3+...+w_{10}x^{10}\]而$H_2$可以表示为:
\[H_2 = w_0+w_1x^1+w_2x^2\]那么如果限定条件$w_3=w_4=w_5…=w_{10}=0$,那么显然$H_2=H_{10}$。但是这种限制比较苛刻,而且如果加上这种限制跟直接使用$H_2$没有区别,因此我们可以放松限制条件。而是限制成:
\[\sum_{q=0}^{10}(w_q\neq 0) \le 3\]即限定了w不为0的个数,而不是限定必须是高阶的w。这种hypothesis记为$H_{2}^{‘}$,称为sparse hypothesis set。他与$H_2$和$H_{10}$的关系是:
\[H_2 \subset H_2^{'} \subset H_{10}\]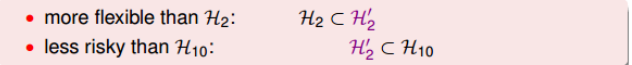
但是sparse hypothesis set $H_{2}^{‘}$还是NP-hard,求解十分困难,所以需要求解一个更加宽松的线性条件Softer Constraint,即
\[\sum_{q=0}^{10}w_q^2 = \Vert w\Vert^2 \le C\]其中C是常数,也就是说所有的权重w的平方和的大小不高于C,这种hypothesis sets记为H(C)。
对于$H^{‘}_2$和H(C)的关系,他们之间有重叠,有交集的部分,但是也没有完全包含的关系,也不一定相等。对于H(C),C值越大,宽松:
\[H(0) \subset H(1.126)\subset...\subset H(1126) \subset ...\subset H(\infty)=H(10)\]所以现在的任务就是求解满足限定条件的权重$w_{reg}$
Weight Decay Regularization
正则化线性回归–岭回归
现在我们的问题就是如下(Z由X转换得来):
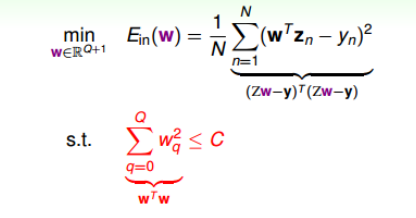
即计算$E_{in}(w)$的最小值,限定条件是$\Vert w^2\Vert \le C$。这个限定条件从几何角度上可以看作被限定在半顶为$\sqrt C$的圆内,而秋外的w都不符合要求。即
\[\min_{w\in R^{Q+1}} E_{in}(w) = \frac{1}{N}(Zw-y)^T(Zw-y) \ s.t. \ w^Tw\le C\]我们可以通过几何化的来求解最小化$E_{in}(w)$的过程。

如果没有限定条件,我们会抵达谷底$W_{lin}$,但是如果有了限定,我们的w被限定在一个圆内,当我们到达圆环时,我们就不能仍然延负梯度方向进行(会跑出圆),而是沿着圆的切线进行,并且一旦某一点w的法线指向谷底,也就意味着我们的w取得了最优值。
也就是说当我们到达某一点使得梯度的沿切线方向没有不为0的分量,即$w_{reg}$和$\bigtriangledown E_{in}(w_{reg})$方向相同时,达到最优解
\[\bigtriangledown E_{in}(w_{reg}) + \frac{2\lambda}{N}w_{reg} = 0\]其中$\lambda$称为Lagrange multiplier。$\frac{2}{N}$方便后面推导。
线性回归的$E_{in}$为:
\[E_{in} = \frac{1}{N}\sum_{n=1}^{N}(Z_n^Tw-y_n)^2\]将梯度带入可得:
\[\frac{2}{N}(Z^TZw_{reg} - Z^Ty) + \frac{2\lambda}{N}w_{reg} = 0\]因此$w_{reg}$为:
\[w_{reg} = (Z_TZ + \lambda I)^{-1}Z^Ty\]统计学上把这个叫做岭回归(ridge regression),也就是带有L2正则化的线性回归。
正则化逻辑回归
对于更一般的问题,如逻辑回归,则可以从另一个角度入手: \(\bigtriangledown E_{in}(w_{reg}) + \frac{2\lambda}{N}w_{reg} = 0\)
因为$\bigtriangledown E_{in}$是$E_{in}$对$w_{reg}$的导数,而$\frac{2\lambda}{N}w_{reg}$可以看成是$\frac{\lambda}{N}w_{reg}^2$的导数,因此,平等式左侧可以看成一个函数的导数,导数为0,即求导数的最小是,最后也就转换为了最小化一个函数:
\[E_{aug}(w) = E_{in}(w) +\frac{\lambda}{N}w^Tw\]其中第二项就是限定条件regularizer,也称谓weight-decay regularization。这个函数被称为Augmented Error,即$E_{aug}(w)$。而其中的$\lambda$就限定了正则化程度
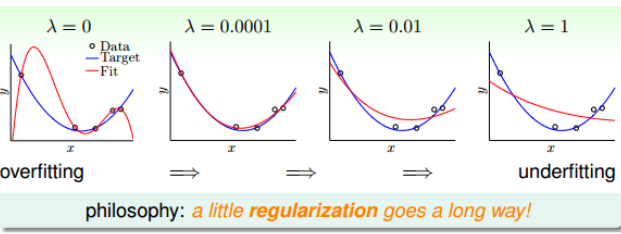
Regularization and VC Theory
那么加上正则化之后,对于VC理论是否有影响,已知
\[E_{aug}(w) = E_{in}(w) +\frac{\lambda}{N}w^Tw\]而VC bound为:
\[E_{out}(w) \le E_{in}(w)+\Omega(H)\]其中$w^Tw$表示的是单个hypothesis的复杂度,记为$\Omega(w)$,而$\Omega(H)$ 表示整个hypothesis set的复杂度。根据两个表达式,$\Omega(w)$包含在$\Omega(H)$之内,所以$E_{aug}(w)$比$E_{in}$更接近于$E_{out}$。
同时根据VC Dimension理论,整个hypothesis set的$d_{vc}=d+1$。这是因为所有的w都考虑了,没有限制条件,而引入限制条件的$d_{vc}(H(C))=d_{EFF}(H, A)$,即有效的VC dimension。当$\lambda >0$时,有
\[d_{EFF}(H, A) \le d_{vc}\]General Regularizers
通用的Regularizers,即$\Omega(w)$,一般有三种形势
- target-dependent
- plausible
- friendly

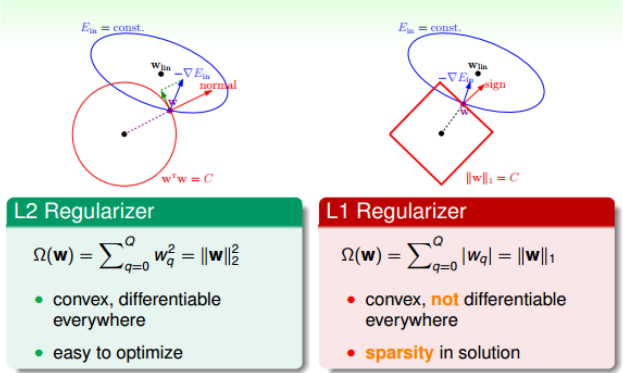
其中常用的是L1和L2
\[L1: \Omega(w) = \sum_{q=0}^Q\vert w_q\vert = \Vert w\Vert_1 \\ L2:\Omega(w) = \sum_{q=0}^Q\vert w_q^2\vert = \Vert w\Vert_2^2\]其中L2是凸函数,比较平滑,易于微分,容易进行最优化计算。
L1计算的不是w的平方和,而是绝对值和,也是凸函数,他所围成的是正方形,因此,在正方形的四个顶点出,是不可微分的。因此它的解一般都在四个顶点上,因为正方形边界处的绝对值都不为0,若$-\bigtriangledown E_{in}$不与其平行,那么w就会向顶点处移动,所以,L1的解是稀疏的,称为sparsity,优点是计算速度快。