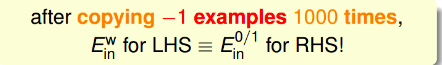机器学习(1)-机器学习的可行性

• 机器学习真的可行吗
• 霍夫丁不等式(Hoeffding’s inequality)
• 单假设函数下的错误率验证
• 多假设函数下的错误率验证
• 无限大假设函数下机器学习的可行性
  • Effective Number of Hypothesis
  • break point
  • Bounding Function: Basic Cases
• The VC Dimension
  • VC Dimension
  • VC Dimension of Perceptrons
  • Interpreting VC Dimension
• Noise and Error
  • Error
  • Algorithmic Error Measure
  • weighted classification
• 参考文章

机器学习真的可行吗

机器学习只有在加上一定的假设条件才是可行的。例如下图

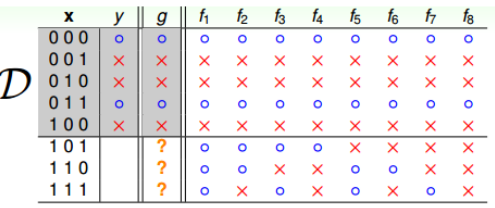
尽管我们的假设函数g可以完美的预测前五个数据，但是对于后三个数据我们的预测并不一定成立，总能找到一个f，使得$f\approx g$不成立。

在D以外的数据中更接近目标函数似乎是做不到的，只能保证对D有很好的分类效果。机器学习的这种特性被称为No Free Lunch(没有免费午餐)。因此NFL特性告诉我们，我们只有加上一定的假设函数才能保证机器学习算法在D之外的数据集上一定能分类或预测成功。

霍夫丁不等式(Hoeffding’s inequality)

以瓶中小球的概率，我们引出霍夫丁不等式，其中，从罐子中随即取出N个球，作为样本。

这N个球中橙色球的比例为u，罐中橙球的比例为v。

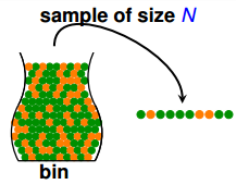
通过霍夫丁不等式推出， u与v接近。

我们称$u=v$是PAC(probably approximately correct)的

单假设函数下的错误率验证

将机器学习问题类比到罐子问题，我们也可以得到相同的结论

• 从 罐子中取出的弹球 –> 训练样本D

• 橙色小球 –> h(x)与f不相等

• 绿色小球 –> h(x)与f相等

同时，我们定义一些参数:

• 分类器的实际错误率：$E_{out}(h) =P(h(x) \neq f(x)) = \mathop{\epsilon} \limits_{X \sim P}\left[\left\vert h(x) \neq f(x)\right \vert \right]$。

• 分类器在抽出样本中的错误率: $E_{in}(h) =P(h(x) \neq f(x)) =\frac{1}{N}\sum \limits_{n=1}^N\left[\left \vert h(x) \neq f(x)\right\vert \right]$。

因此，我们利用霍夫丁不等式，可以得到:

即这个不等式表明, $E_{in}(h) = E_{out}(h)$也是PAC的。

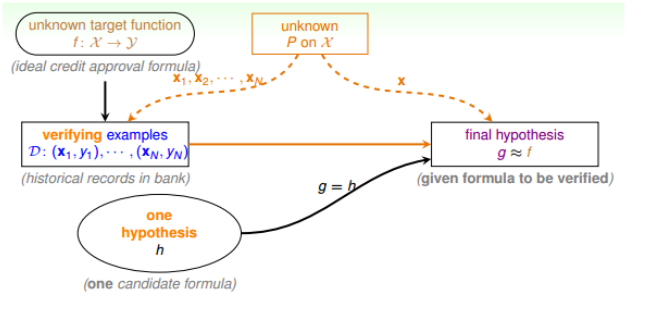
但是这并不意味着,当$E_{in}(h) \approx E_{out}(h)$的时候，$g\approx f$， 因为，这并不能保证$E_{in}(h)$足够小，如果我们的预测的h的错误率很大，这显然不是一个好的选择。所以，我们一般会通过学习算法A，选择最好的h， 使$E_{in}(h)$足够小。 从而保证$E_{out}(h)$很小。为了得到最小的$E_{in}(h)$， 我们添加的验证过程。

多假设函数下的错误率验证

上一个我们仅仅是针对单一的假设h，而且通过霍夫丁不等式可以得出$E_{in}(h) \approx E_{out}(h)$。但是在实际工程中，假设并不仅仅一个，所以，哪怕$E_{in}(h) \neq E_{out}(h)$的概率再小，随着h数量的增加，总有可能出现。

以投硬币为例，150人抛硬币，每人抛5次，其中至少有一个人连续五次都是正面的可能性为:

我们称这个现象为BAD sample，如果我们以正面为$E_{in}(h)$， 那么可见$E_{in}(h) = 0$， 但他对于真实现象不具有代表性。而这种情况对机器学习的伤害也是巨大的。

那么在机器学习过程中，如果BAD sample的可能性很小，我们也可以在一定程度上保证机器学习的可能性。

我们假设假设函数之间是没有交集的，那么在有限的假设函数下，根据union bound规则。我们可以推导出

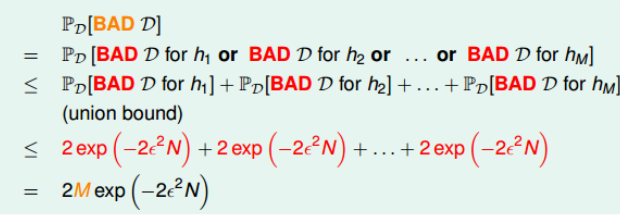
所以在有限M个的假设函数，并且N足够大，那么演算法A随即选择的一个g，都有足够的概率保证$E_{in}(h)\approx E_{out}(h)$。因此，我们只需要找到一个g，保证$E_{in} \approx 0$即可。

无限大假设函数下机器学习的可行性

有限个假设函数下，霍夫丁不等式为:

但是我们的推导过程中

如果$M=\infty$，上面不等式右边的值将会很大，但是这个推导过程中，我们假设了各个假设函数之间没有交集，实际上，很多情况下是有交集的。

因此，如果我们找出交集，将其分为有限个类别。那么也可以保证机器学习的可行性

对于二分类问题，我们的，一个训练样本的结果只有-1和+1， 因此最多的分类最多有$2^N$个，但是，随着N的增加，其分类还要小于$2^N$， 例如当N=4时，其最多有14类。

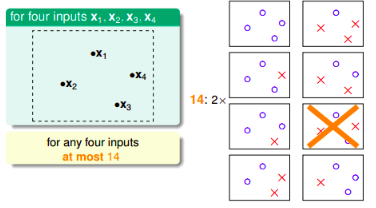
我们定义effective(N)为N个点的最多分类情况，那么霍夫丁不等式可以写作

已知$effective(N) < 2^N$，如果能够保证$effective(N) \ll 2^N$， 那么就可以保证右边接近于0。

Effective Number of Hypothesis

再次提出两个参数:

• 二分类(dichotomy)。就是将空间中的点用一条直线分为正类和负类。dichotomy H就是平面上能将点完全用直线分类的直线种类，在上面可以推知，他最大为$2^N$。我们的研究目标就是使用dichotomy代替M。
• 成长函数(growth function): 记为$m_H(N)$。对于由N个点组成的不同集合中，某集合对应的dichotomy最大，那么这个dichotomy值就是$m_H(N)$。$m_H(N) = \max\limits_{x_1, x_2, ..x_n\in \chi}\vert H(x_1, x_2, .., x_n)\vert$。

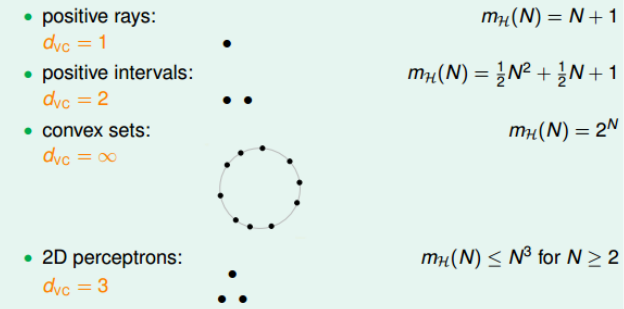
例如

其中，前两个是多项式的，可以使用$m_H(N)$来替代M，而convex sets是不满足的。现在需要探讨2D perceptrons是多项式还是指数形式的。

break point

再次定义一个参数:

• break point: 满足$m_H(N) \neq 2^N$的N的最小值就是break point， 称为k。

因此，上述四种情况的break point为：

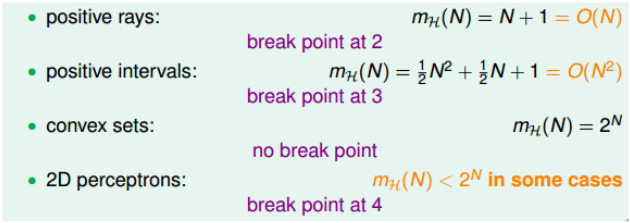
Bounding Function: Basic Cases

影响$m_H(N)$的参数有N和break point k。

因此定义一个参数：

• bounding function:B(N, k)，当break point为k时，成长函数$m_H(N)$可能的最大值， 即B(N, k)是$m_H(N)$ 的上届。

因此新目标为$B(N, k) \le poly(N)$

对于B(N, k)有知

• 当k=1, B(N, k) = 1。
• 当N<k时， $B(N, k) = 2^k$。
• 当N=k时， $B(N, k) = 2^k-1$。
• 当N>k时，$B(N, k) \le B(N-1, k) + B(N-1, k-1)$。

综上，可得:

那么上述不等式右边最高阶为k-1的N多项式，因此B(N, k)的上届满足多项式poly(N)。 即:

现在就可以将$m_H(N)$来替代M了。即，我们想要:

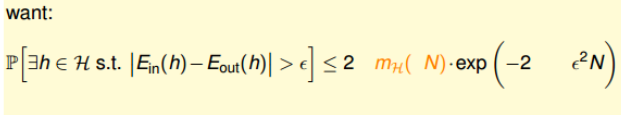
实际上的表达式经过经过推导为:

最终，我们通过引入成长函数$m_H$，得到了一个新的不等式，称为 VC bound：

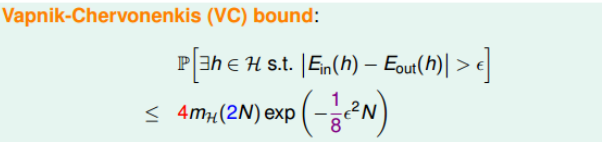
The VC Dimension

我们知道如果一个假设空间H对于采样样本D有break point k，那么他的成长函数是有界的，他的上届成为bound function。而bound function也是有界的，其上届为$N^{k-1}$，且，$N^{k-1}$比$B(N, k)$松弛的多。

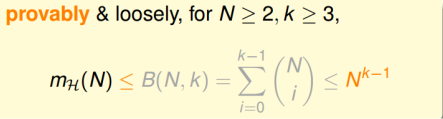
因此，VC bound可以转换为: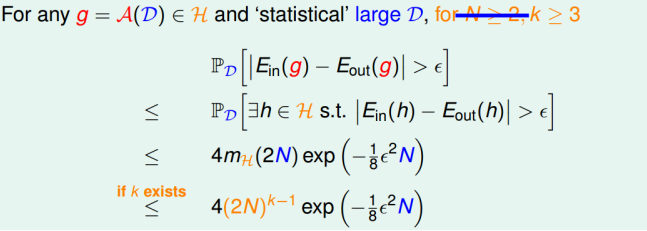

因此，不等式只与N和k有关了，一般N足够大，所以只考虑k值。

• 若假设空间H有break point k,且N足够大,则根据VC bound理论,算法有良好的泛化能力
• 在假设空间中选择一个矩g,使$E_{in}\approx 0$，则其在全集数据中的错误率会较低

VC Dimension

定义一个新的名词:

• VC dimension: 指某假设集H能够shatter的最多inputs的个数，即最大完全正确的分类能力，即为$d_{vc}$。例如对于二元分类问题，对N个输入，如果能够将$2^N$种情况都列出来，则称N个输入能够被假设集H shatter。

那么根据break point的定义: $d_{vc} = k-1$。

那么现在，VC bound就跟$d_{vc}$和N有关了。因此，如果一个假设集H的$d_{vc}$确定了，则就能满足机器能够学习的第一个条件$E_{out} \approx E_{in}$。

VC Dimension of Perceptrons

我们在前文推论的都是2D perceptrons。那么在多维情况下呢。我们只要保证存在$d_{vc}$就可以保证机器学习的可行性，而经过推论，我们知道$d_{vc} = d+1$。推论过程

因此，对于多维感知器，我们仍然能确保机器学习的可行性。

但是我们仍然需要注意，我们要选择合适的$d_{vc}$。

Interpreting VC Dimension

我们引入一个$\delta$:

即出现BAD的概率最大不超过$\delta$。重新考虑一下$\epsilon$。

$\epsilon$表现空间H的泛化能力，$\epsilon$越小，泛化能力越大。

同时，我们也可以得到(因为我们更考虑上届)：

其中第二项是模型复杂度(model complexity)，其与样本数量N,假设空间H( $d_{vc}$)， $\epsilon$有关。而$E_{out}$、模型复杂度，$E_{in}$与$d_{vc}$的关系为:

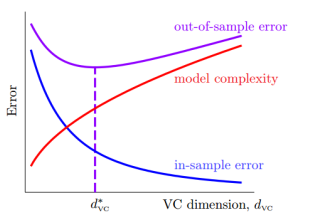
有图可得:

• $d_{vc}$越大，$E_{in}$越小，$\Omega$越大
• $d_{vc}$越小，$E_{in}$越大，$\Omega$越小
• 随着$d_{vc}$增大，$E_{out}$先减小后增大

所以，为了得到合适的$E_{out}$， 我们需要选择合适的$d_{vc}$。

除了$d_{vc}$，还有N会影响到机器学习的能力。当$d_{vc}$给定后，我们的样本数量N可以通过VC bound计算得出。其理论值为$10000d_{vc}$，这是因为VC bound过于宽松了 ，实际上，大概只需要$10d_{vc}$即可。

虽然VC bound比较宽松，但是基本上对所有模型的宽松程度是基本一致的，所以，不同模型之间还是可以进行横向比较的。因此 VC bound宽松对机器学习的可行性没有太大影响。

Noise and Error

上文中的证明是在数据集中没有Noise的情况下进行的，但是现实世界中，我们总会存在noise.

• 由于人为因素，正类被误分为负类，或着负类被误分为正类
• 同样特征的样本被模型分为不同的类
• 样本的特征被错误的记录和使用

因此，我们的理想目标f(x)和标签$y_n$很有可能是不一致的。所以，对于一个点，他不是一个确定的，而是一种概率。即对每一个(x, y)出现的概率为$P(y\vert x)$。但是此时VC Dimension仍然成立。

$P(y\vert x)$称之为目标分布(target distribution)。它实际告诉我们最好的选择是多少，同时伴随着多少noise。他可以被看成”ideal mini-target”+noise。比如:

我们的目标就改为了预测”ideal mini-target”, (f(x))。

Error

机器学习考虑的是找出假设函数g与目标函数f有多相近。在前文我们使用$E_{out}$。而实际上g对错误的衡量有三个特性:

• out-of-sample： 样本外的未知数据
• pointwise： 对每个数据点x进行测试
• classification： 看prediction和target是否一致，一般classification error通常称为0/1 error

pointwise error是机器学习中最常用也是最简单的一种错误衡量方式,$E_{in}$和$E_{out}$的表达式为:

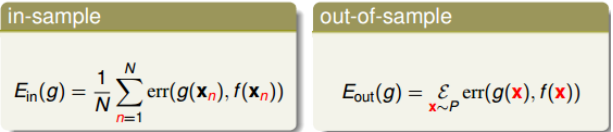
其分类和回归问题的err计算为。

Algorithmic Error Measure

Error有两种，false accept和false reject。

对于不同的错误，在不同的场景中，我们有不同的权重，比如如果是安保系统，那么false accept应该设置的大一些。

机器学习演算法A的cost function error估计的方法有多种，常用的方法是pausible或者friendly。根据具体情况而定。

引入之后，学习流程图为:

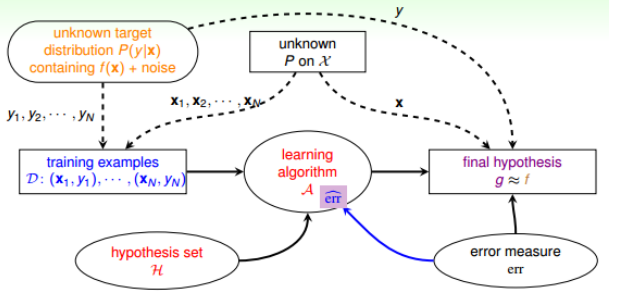
weighted classification

cost function中，false accept和false reject赋予不同的权重，在演算法中体现。对不同权重的错误惩罚，可以选择vitual copying的方法。

参考文章

本系列学习笔记是通过学习林轩田的课程，并且参考了红色石头的笔记