因为神经网络还是比较熟悉的,所以,就简单记录下反向传播算法吧
神经网络
对于一个简单的神经网络,如图:
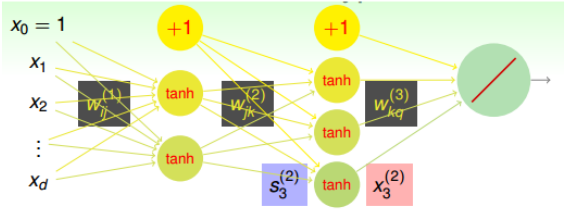
其中:
- x1~xd是我们的输入。
- $d^{(l)}$是指我们在第l层的神经元个数(包括偏置,置$x_0=1$), 其中l从0计数,当l为0时,表示输入层
- $w_{ij}^{(l)}$表示第l层的权重。
- $s_i^{(l)}$表示第l层,第i个单元的输入
- $x_j^{(l)}$表示第l层,第j个单元的输出
显然,对于每一层的分数(输入)s,他的表达式为:
\[s_j^l = \sum_{i=0}^{d^{(l-1)}}w_{ij}^{(l)}x_i^{(l-1)}\]而我们每一层的输出是:
\[x_j^{(l)} = tanh(s_j^{(l)}) \ \text{其中 l<L}\]而最后一层,试不同的作用,我们选择不同的激励函数,以线性回归为例,我们的最后一层的激活 函数为$\theta(x)=x$.
也就是说我们最终的output为:
\[Output = s^{(L)}\]反向传播算法
我们以输出层的激活函数为线性的距离,那么我们的目标就是:
\[\min E_{in}(x) = \sum_{n=1}^N(y_n-\text{NNet}(x_n))^2\]我们令$e_n = (y_n-\text{NNet}(x_n))^2$, 显然可以得到:
\[e_n = (y_n-\text{NNet}(x_n))^2 = (y_n-s_1^{(L)})^2 = (y_n-\sum_{i=0}^{d^{(L-1)}}w_{i1}^{(L)}x_i^{(L-1)})\]显然对于这一点,我们可以通过梯度下降的方法来得到$w_{il}^{(L)}$.
我们计算$e_n$和$w_i1^{(L)}$的偏导:
\[\begin{align} &\frac{\partial e_n}{\partial w_{i1}^{(L)}}\\ =&\frac{\partial e_n}{\partial s_{1}^{(L)}}*\frac{\partial s_1^{(L)}}{\partial w_{i1}^{(L)}}\\ =& -2(y_n-s^{(L)}_1) *(x_i^{(L-1)}) \end{align}\]显然我们可以使用梯度下降的方法求解出$w_{i1}^{L}$, 但是对于隐藏层的权重,我们是否仍然可以求得,我们首先令$e_n$与第l层第j个神经元的分数$s_j^{(l)}$的偏导为$\delta_j^{(l)}$,
\[\frac{\partial e_n}{\partial s_{j}^{(l)}} = \delta_j^{(l)}\]则$e_n$对$w_{ij}^{(l)}$的偏导为:
\[\begin{align} &\frac{\partial e_n}{\partial w_{ij}^{(l)}}\\ =&\frac{\partial e_n}{\partial s_{j}^{(l)}}*\frac{\partial s_j^{(l)}}{\partial w_{ij}^{(l)}}\\ =& \delta_j^{(l)}*(x_i^{(l-1)}) \end{align}\]现在,我们的目标就转变为了求$\delta$了。
因为我们的神经网络的计算是有序的,也就是如下图所示,第l层第j个神经元的分数经过tanh函数,得到该层的输出$x_j^{l}$, 然后再与下一层的权重$w_{jk}^{(l+1)}$相乘得到第l+1层的分数$s_j^{l+1}$,直到最后$e_n$.
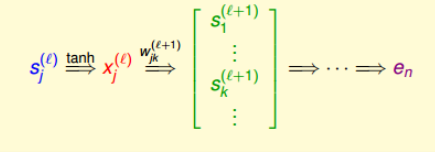
那么显然
\[\delta_j^{(l)} = \frac{\partial e_n}{\partial s_{j}^{(l)}} = \sum_{k=1}^{d^{(l+1)}}\frac{\partial e_n}{\partial s_{j}^{(l+1)}}*\frac{\partial s_k^{(l+1)}}{\partial x_{j}^{(l)}}*\frac{\partial x_j^{(l)}}{\partial s_{j}^{(l)}}\\ = \sum_K \delta_k^{(l+1)}*w_{jk}^{(l+1)}*(tanh^{'}(s_j^{l}))\]所以,我们的$\delta^{(l)}$与$\delta^{l+1}$的关系,这意味着,只要我们得到输出层的$\delta^{L}$, 我们就一可以一层一层的推导,然后得到$e_n$对各个$w_{ij}^{(l)}$的偏导数,然后我们就可以使用梯度下降进行权重的迭代优化。
这种算法就被称为反向传播算法(Backpropagation Algorithm)。
其算法过程:
初始化所有的权重 $w_{ij}^{l}$
for t = 0, 1, …., T:
- 前向传播,计算所有的$x_i^{(l)}$和$s_i^{(l)}$
- 反向传播, 计算所有的$\delta_j^{(l)}$
- 梯度下降: $w_{ij}^{l} \leftarrow w_{ij}^{l}-\eta x_i^{(l-1)}\delta_j^{(l)}$
得到我们的最终结果G(x)
优化与正则化
因为神经网络是油输入层,多个隐藏层,输出层构成的,是一个复杂的非线性结构。因此$E_{in}$可能有多个局部最小值,是non-convex, 所以找到全局最小值是非常困难的。
对于这个问题,不同的初始权重会得到不同的局部最小值,所以对于初始权重的设置就显得十分重要,我们有不同的方法设置权重,但是不再此处说明。
此外,对于tanh这样的激活函数,其对应的整个模型复杂度为$d_{vc}=O(VD)$, 其中V是神经网络中神经元的个数,D是所有权值的个数,显然$d_{vc}$是很有可能非常大的,为了防止这种可能,我们同样可以进行正则化。
但是已有的L2正则化,是对每个权重等比例缩小的,即大的权重缩小程度大,小的权重缩小程度小。这就导致了很难得到值为0的权重,而我们恰恰希望某些权重$w_{ij}=0$, 从而减少计算量,也减少模型复杂度,即权重的解是松散(sparse)的
而L1虽然可以得到sparse解,但是它很难求导,所以一个更好的选择是weight-elimination regularizer。它类似L2, 只不过在L2上做了尺度的缩小,使得large weight和small weight都能得到同等程度的缩小。
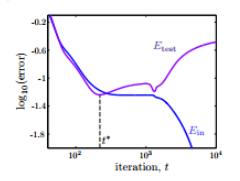
\[\sum \frac{(w_{ij}^{(l)})^2}{1+(w_{ij}^{(l)})^2}\]除此之外,我们还有一个很有效的正则化方法,就是early stopping。就是说,在神经网络训练中次数t不能太多。因为,t太大的时候,相当于给模型找到最优值更多的可能性。模型更复杂