逻辑回归
在二元分类问题中,我们将数据分为-1和+1,但是在某些情况下,我们更关心概率,比如,我们想知道的不是患者有没有心脏病,而是患者有多大的概率是心脏病。这种问题也被成为软性二元分类问题(‘soft binary classification’)。
此时,我们的目标函数就变为了:
\[target \ function \ f(x) = P(+1\vert x)\in [0, 1]\]模型
我们仍然对所有的特征值进行加权处理。计算的结果,我们称之为”risk score”。也就是加权和越高,说明越容易患病。
\[s = \sum_{i=0}^dw_iX_i\]但是$s\in(-\infty,+\infty)$, 如果能够将其映射到(0, 1)区间,显然我们的最终结果会更加形象。
Sigmoid Function
一种方法是使用Sigmoid Function,记为$\theta(s)$。因此我们的目标就成了找到一个hypothesis:$h(x) = \theta(w^Tx)$
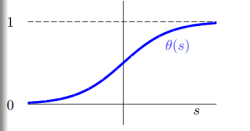
一个常用的sigmoid function就如上图一样,且其函数为:
\[\theta(s) = \frac{1}{1+e^{-s}}\]所以,我们的预测函数就变为了
\[\theta(x) = \frac{1}{1+e^{-w^Tx}}\]Logistic Regression Error
知识补充:最大似然估计
对于逻辑回归,我们使用一个”似然性”的概念来描述我们的Error。目标函数$f(x) = p(+1\vert x)$ ,如果我们找到了hypothesis很接近target function。也就是说,在所有的Hypothesis集合中找到一个hypothesis与target function最接近,能产生同样的数据集D,包含y输出label,则称这个hypothesis是最大似然likelihood。
对于一个样本集,我们的目标函数$f(x)=p(+1\vert x)$,通过转换我们可以得到:

如果有一个数据集为
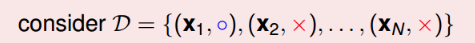
所以我们生成数据集D的概率为:
\[p(x_1)f(x_1) × p(x_2)(1-f(x_2) ... × p(x_N)(1-f(x_N)))\]但是我们的f(x)是未知的,所以,如果我们能够求出来一个h(x)能够使得生成数据集D的概率是最大的,这也是可以接受的。
\[p(x_1)h(x_1) × p(x_2)(1-h(x_2) ... × p(x_N)(1-h(x_N)))\]由于我们逻辑回归中的sigmoid function具有一个特性$1-h(x) = h(-x)$。
所以,我们的最终的似然性为:
\[likelihood(h) = p(x_1)(+x_1) × p(x_2)h(-x_2)×...p(x_N)h(-x_N)\]我们的目标就是为了使其乘积最大化,因为对于所有的h,p(x)是确定的,所以

最终我们代入相应公式,可以将其转换为一个minimize问题:
第一步, 取ln, 得$\sum_{n=1}^N\ln(h(y_nx_n))$
第二步, 代入$h(x) = \theta(w^Tx)$
\[\begin{align} & \sum_{n=1}^N\ln(h(y_nx_n)) \\ = & \sum_{n=1}^N\ln((1+\exp(-y_nw^Tx_n))^{-1})\\ =& -\sum_{n=1}^N\ln((1+\exp(-y_nw^Tx_n))) \end{align}\]第三步, 取个负号,将max转换为min
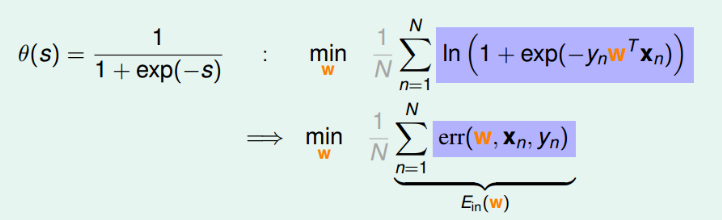
对于其中的err,我们称之为交叉熵误差(cross-entropy error)
梯度下降
现在我们已经明确了$E_{in}$了,
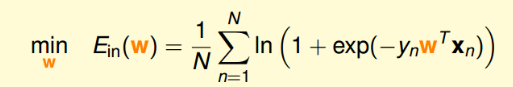
当然,逻辑回归中的$E_{in}$也是连续的,可微的,二次可微的凸函数,所以,我们也可以计算$E_{in}$的梯度为零时的w,即为最优解。
\[\begin{align} \frac{\partial{err}}{\partial w} & = \frac{-y_nx_n\exp(-y_nw^Tx_n)}{1+\exp(-y_nw^Tx_n)} \\ &=\frac{-y_nx_n}{1+\exp(y_nw^Tx_n)}\\ &=(-y_nx_n)\theta(-y_nw^Tx_n) \end{align}\]通过求解,其梯度表达式为:
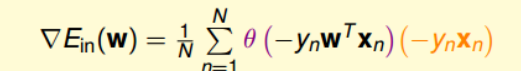
对于这个公式,我们让其所有的点都为0是不太现实的。
所以,我们使用迭代的思想,即迭代更新w,使其逼近最优解。
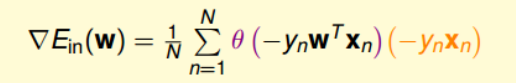
我们的目标是使$E_{in}$越来越小,因此,我们就需要使$E_{in}(w_t+\eta v) < E_{in}(w_t)$。
根据泰勒展开,我们的$E_{in}(w_t+\eta v)$就展开成为:
\[E_{in}(w_t+\eta v) \approx E_{in}(w_t) + \eta v^T\bigtriangledown E_{in}(w_t)\]为了保证$E_{in}$越来越小,我们需要使$v$与$\bigtriangledown E_{in}(w_t)$方向相反,他们的内积为负。所以下降方向v为:
\[v = -\frac{\bigtriangledown E_{in}(w_t)}{\| \bigtriangledown E_{in}(w_t) \|}\]所以梯度下降最终结果为:
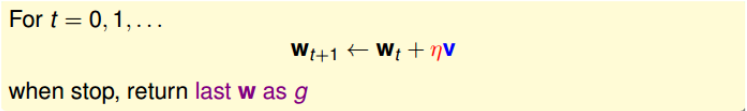
学习速率
对于不同的$\eta$,显然学习的过程是不一样的
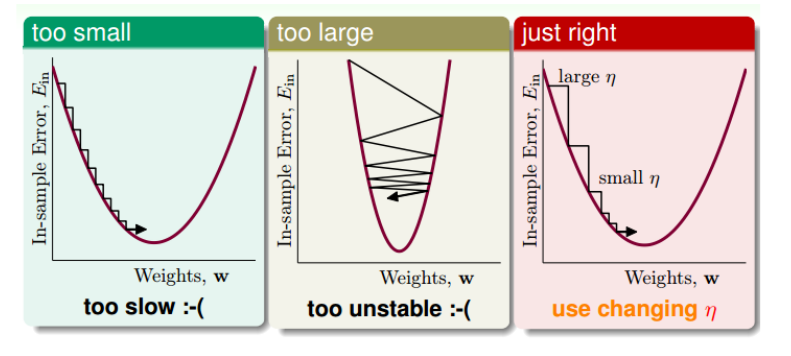
最好的结果是随着不同的梯度大小,其有不同的值,因此我们可以令:
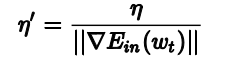
所以最终的梯度下降中的迭代公式为:
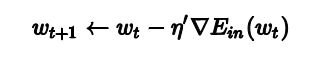
算法过程
- 初始化$w_0$
- 计算梯度$\bigtriangledown E_{in}(w_t) = \frac{1}{N}\sum_{n=1}^{N}\theta(-y_nw_t^Tx_n)(-y_nx_n)$
- 更新迭代$w_{t+1} \leftarrow w_t - \eta \bigtriangledown E_{in}(w_t)$
- 满足$\bigtriangledown E_{in}(w_t) \approx 0$或者达到一定的迭代次数,即可结束\
补充
需要注意的是:不同的标签,其梯度是不同的,比如,在吴恩达课程里,其标签是{0, 1},所以吴恩达视频中,cost function或者$E_{in}$是:
\[E_{in} = \frac{1}{m}\sum_{i=1}^{m}[-y_i ln(h(x_i)) - (1-y_i)ln(1-h(x_i))]\]而梯度为:
\[\bigtriangledown E_{in}(w_t) = \frac{1}{m}\sum_{i=1}^{m}(h(x_i)-y_i)x_i\]吴恩达的比较好实现,所以,推导一下,用来支持它
从似然估计开始我们的目标是得到最大的likelihood(h):
\[likelihood(h) = p(x_1)h(x_1) × p(x_2)(1-h(x_2) ... × p(x_N)(1-h(x_N)))\]所以
\[\max_h \ \ likelihood(h) \propto h(x_1)h(1-x_2)...h(1-x_n)\]所以,就可以表示为:
\[\prod_{i=0}^{n:y=1}h(x_i)×\prod_{i=0}^{n:y=0}h(((1-x_i)\]通过取ln将连乘符号改为连加符号
\[\sum_{i=0}^{n:y=1}ln(h(x_i)) + \sum_{i=0}^{n:y=0}ln(h(1-x_i))\]第一个连加符号是y=1的,第二个连加符号是y=0的,所以,我们可以将其合并得到
\[\sum_{i=1}^{m}[y_i ln(h(x_i)) +(1-y_i)ln(1-h(x_i))]\]所以,我们最终的$E_{in}$就变成了
\[E_{in} = \frac{1}{m}\sum_{i=1}^{m}[-y_i ln(h(x_i)) - (1-y_i)ln(1-h(x_i))]\]求个梯度就可得:
\[\bigtriangledown E_{in}(w_t) = \frac{1}{m}\sum_{i=1}^{m}(h(x_i)-y_i)x_i\]