线性回归
Hypothesis
线性回归问题中,我们可以对我们的特征求权重和,然后将我们的权重和作为我们的预测
我们假设特征向量为$x = (x_0, x_1, …, x_d)$, 那么我么你的权重和为:
\[y \approx \sum_{i=0}^dw_ix_i\]通过向量表示,我们的线性回归hypothesis为:$h(x) = w^Tx$。
Error Measure
对于线性回归问题,我们一般使用squared error。

为了实现机器学习,我们的目标就是最小化$E_{in}(w)$
优化–最小二乘法
求解最小化$E_{in}(w)$的过程就是一个优化的过程。
在这里我们使用最小二乘法的方法对线性回归问题进行优化求解w。其最终结果为$w = (X^TX)^{-1}X^Ty$
其推理过程如下:
-
首先将$E_{in}(w)$转化为矩阵的形式。
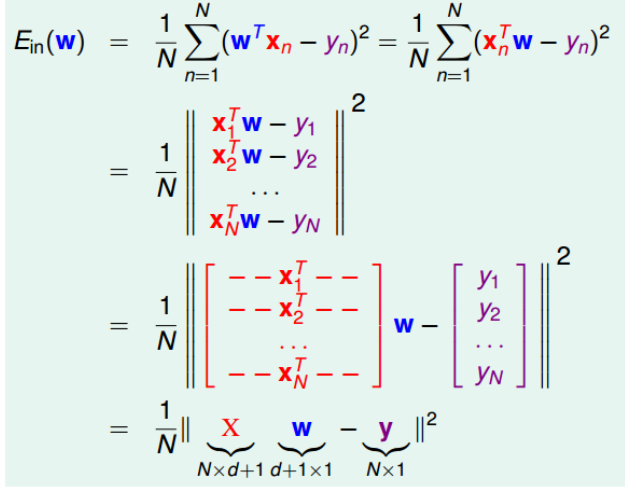
-
求偏导
一般而言,此类线性回归问题是一个凸函数,这意味着,我们找到一阶导数为零的位置就找到了最优解

我们首先将$E_{in}(w)$展开

那么我们求解的梯度为:
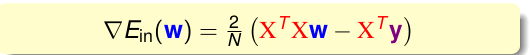
令其等于0,则可以求得:
一般情况下,由于样本数量N一般远大于样本特征维度d+1, 所以能够保证矩阵的逆是存在的,我们成这样的矩阵为非奇异矩阵。
线性回归的可行性
机器学习需要保证两个问题一个是$E_{in }$最小, 一个是$E_{in} \approx E_{out}$, 通过最小二乘法,我们可以保证第一个条件,我们主要要分析第二个条件。
使用$E_{in}$的均值来求解。我们抽取不同的样本,然后分别求解$E_{in }$,最后求解平均即可。

我们令$H = XX^+$, 并称它为帽子函数。则
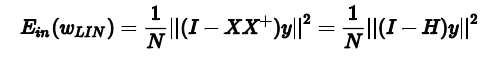
我们可以通过几何图形的角度进一步求解$E_{in}$。(推理过程见笔记或课程)最终我们可以求出:
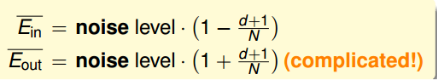
其学习曲线为:
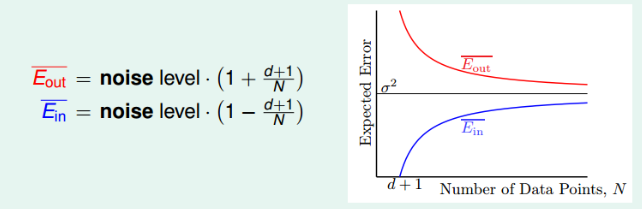
随着N的增加,两者越来越靠近。