Large-Margin Hyperplane
在现实世界中,样本中存在噪声是一种十分普遍的线性,为了保证我们对噪声的容忍度。如下图,图三对噪声的容忍度最高,其可视化就是原本所在的圆形区域。
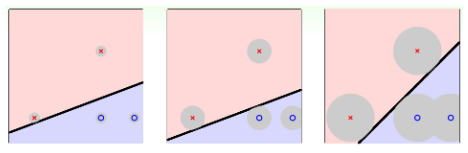
很明显,圆形区域越大,意味着样本点理直线越远,因此,我们可以将问题转换,得到一个胖的直线,越胖则容忍误差的能力越强。这个胖的程度我们用margin表示。
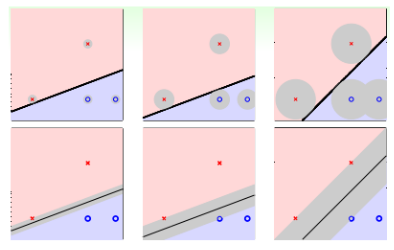
使用数学符号表示,就是找到一个分类正确的直线,并且保证margin最大。即,找到一个离分类线最近的点到分类线距离最大。

为了方便计算,我们首先将w进行转化$[w, b]$。即将$b=w_0$,这样可以省去$x_0$。因此hypothesis变为$h(x) = sign(w^Tx+b)$。

找到一个离分类线最近的点到分类线距离最大。那么可视化的观察一下:对于一个分类平面(其中w是平面的法向量),我们该如何找到平面外一点到平面的距离呢?
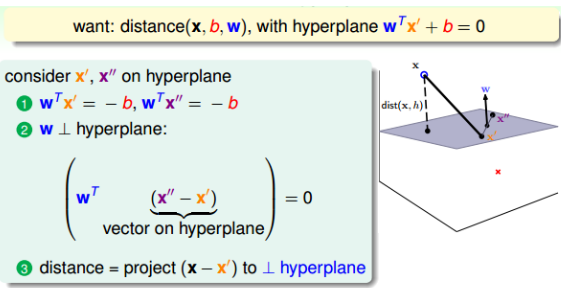
由图可以看出,其最终距离为:
\[\begin{equation} \begin{split} dist(x, b, w) &= \vert (x-x^{'})cos(\theta)\vert \\ &= \vert \Vert x-x^{'}\Vert *\frac{(x-x^{'})w}{\Vert x-x^{'}\Vert *\Vert w\Vert}\vert \\ &=\frac{1}{\Vert w\Vert}\vert w^Tx-w^Tx^{'}\vert\\ &=\frac{1}{\Vert w\Vert}\vert w^Tx+b\vert \end{split} \end{equation}\]又因为要保证所有的点都分类正确,即$y_n(w^Tx_n+b)>0$,显然,我们可以去掉我们的绝对值。
\[dist(x, b, w) = \frac{1}{\Vert w\Vert}y_n(w^Tx_n+b)\]因此,我们的margin为$margin(b, w) = \max\limits_{n=1…N} \frac{1}{\Vert w\Vert}y_n(w^Tx_n+b)$
为了简化计算,由于分类面$w^Tx+b=0$和$3w^Tx+3b=0$是一样的。那么我们直接令离分类面最近的点为$y_n(w^Tx_n+b)=1$。因此,我们的margin(b, w)就变为了:$margin(b, w)=\frac{1}{\Vert w\Vert}$。
此时,我们的目标就变成了
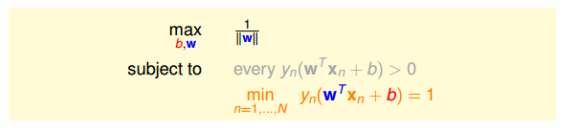
为了进一步简化,将$y_n(w^Tx_n+b)>0$省去,同时最小的为1,也意味着$y_n(w^Tx_n+b)\ge 1$,尽管条件放松了,但是仍然能保证最小值为1。然后最后把最大化问题转为最小化问题,即求$\frac{1}{2}w^Tw$的最小化问题。
所以我们对目标进行转换:
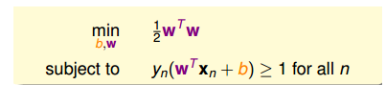
Reasons behind Large-Margin Hyperplane
这种求解大宽度分类器的算法被称为SVM(支持向量机),SVM和正则化十分类似,只不过他的最小化是求解$w^Tw$,而限制变为了$E_{in}=0$。正好与正则化目标和条件对调。

首先考虑一下支持向量机的VC Dimension。由于分类线很胖,那么显然,被shatter的点的个数就可能越少。比如,如果一条线的宽度是1.126,那么右边两种显然是不能被正确分类的。
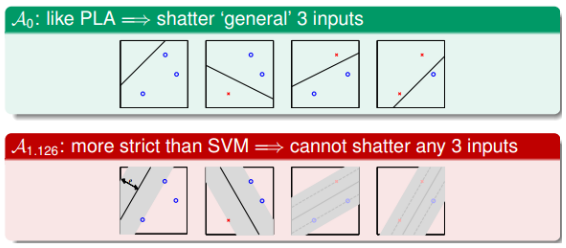
那么显然break point就变小的,有效的VC Dimension也就变小的,得到$E_{out} \approx E_{in}$,模型的泛化能力变强了。
对于之前的感知器模型,他的$d_{vc}=d+1$,那么这里的Large-margin演算法的$d_{vc}(A_p)\le d+1$。VC Dimension减少降低了模型复杂度,提高了泛化能力。
SVM
现在我们已经得知了这种大宽度分类的目标,可以想象对于这种大宽度问题,我们的最终解只跟分类面两边距离最近的几个点有关,决定这个分类面的几个点称为支持向量(Support Vector),而利用他们求解最佳分类面的方法成为支持向量机(Support Vector Machine)。
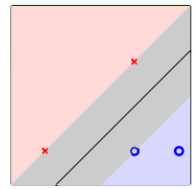
Linear SVM
简单的SVM是一个典型的二次规划问题,即Quadratic Programming(QP)。

所以线性SVM算法可以总结为三个步骤:
- 计算相应的二次规划参数Q,p, A, c
- 根据QP求解b, w
- 根据b, w得到最佳分类面

Dual SVM
如果是非线性的问题,我们也可以通过特征转换,将特征转换到z域中,但是这样也导致了$d_{vc}$变大,如果$d_vc$变得无限大,那么使用QP解法就会很难求解,Dual SVM就是为了求解这种问题的一种尝试。
对偶支持向量机(Dual Support Vector Machine)将对d的依赖转换为了对变量个数N的依赖

因为我们的目标与求解正则化问题十分相似,所以,我们同样可以引入拉格朗日因子(Lagrangian multipliers)。
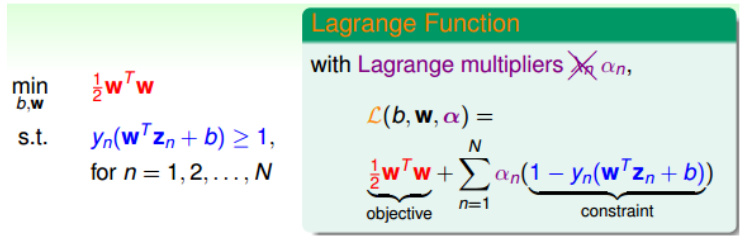
同时,我们将SVM构造成一个非条件问题:

之所以包含最大化问题,是因为我们规定拉格朗日因子$\alpha_n \ge 0$,根据条件$(1-y_n(w^Tz_n+b))\leq0$,如果没有达到最优解,即存在不满足该条件的情况,那么最大值会达到无穷大,所有都有满足,那么显然是满足$(1-y_n(w^Tz_n+b))\leq0$。那么只有当$\sum_n\alpha_n(1-y_n(w^Tz_n+b))=0$有最大值,最大值就是$\frac{1}{2}w^Tw$。
现在的SVM问题已经转化为了
\[SVM = \min_{b, w}(\max_{all \ \alpha_n \ge 0}L(b, w, \alpha))\]那么对任意固定的$\alpha^{‘}$,且$\alpha^{‘}_n\ge 0$,一定有不等式:

进一步转换,不等式也成立:

已知$\ge$是一种弱对偶关系,那么在二次规划QP问题中,如果满足以下三个条件
- 函数是凸的(convex primal)
- 函数有解(feasible primal)
- 条件是线性的(linear constraints)
那么,上述不等式关系就变成强对偶关系,$\ge$变成$=$,即一定满足条件的解(b, w, a),等式左边和右边都成立,我们可以通过右边的形式求解最终答案:
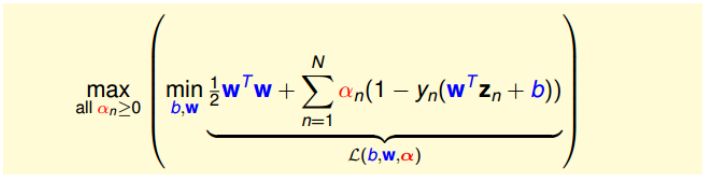
我们需要对这个内容进行进一步的转换,去掉其中的min运算符,因此,我们对参数求梯度并令其为0:
\[\frac{\partial L(b,w,\alpha)}{\partial b}=0=-\sum_{n=1}^N\alpha_ny_n \\ \frac{\partial L(b,w,\alpha)}{\partial w}=0=w-\sum_{n=1}^N\alpha_ny_nz_n\]那么我们现在将这些条件代入,然后就可以去掉min了(因为对b求导等于0.因此里面的最小化问题与b无关,可以消掉b)

因此,我们的问题就转换为了满足三个条件的最大化问题了。
- $all \ \alpha_n\ge0$
- $\sum_{n=1}^N\alpha_ny_n=0$
- $w=\sum_{n=1}^N\alpha_ny_nz_n$
而且只跟$\alpha_n$有关。我们把这种满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)。

Solving Dual SVM
对于上面的最大化问题,我们还可以转化为最小化问题(不懂,但是就只讲了这些):

显然,现在我们可以使用二次规化QP解法来求解这个问题了

所以,使用Dual SVM的计算过程就是:
- 求解Q, p, A, c
- 使用QP求解$\alpha$
- 根据KKT条件,就可以使用w和b。先使用$w=\sum\alpha_ny_nz_n$求解w,然后使用$\alpha_n(1-y_n(w^Tz_n+b))=0$,任取一$\alpha_n\neq0$即$\alpha_n>0$的点,得到$\alpha_n(1-y_n(w^Tz_n+b))=0$,进而求得b。
之所以上述可以使用$\alpha_n(1-y_n(w^Tz_n+b))=0$来求解b,这是因为当$\alpha_n>0$ 时,有$y_n(w^Tz_n+b)=1$一定成立。$y_n(w^Tz_n+b)=1$正好表示的是该点在SVM分类线上,即fat boundary。也就是说,满足$\alpha_n>0$ 的点一定落在fat boundary上,这些点就是Support Vector。
也就是说,分类线上的点不一定是支持向量,但是满足$\alpha_n>0$的点一定支持向量。

既然SV只由$\alpha_n>0$决定,根据KKT,也可以发现w和b仅有SV即$\alpha_n>0$的点决定,简化了计算量。这跟分类线只由旁边界上的点决定是一个道理。也就是说,样本点可以分成两类:一类是support vectors,一类不是support vectors,对求解fattest hyperplane没有影响

对于两种SVM,linear Hard_Margin SVM有d+1个参数, 有N个限制条件。当个d+1很大时,求解困难。而Dual Hard_Margin SVM有N个参数, 有N+1个限制条件。通常,如果N不是很大,一般使用Dual SVM来解决问题。但是需要注意的是在计算$q_{m, n}=y_ny_mz_n^Tz_m$的过程中,由Z向量引入d,实际上复杂度已经隐藏在计算过程中了。
Kernel SVM
Dual SVM虽然已经将从对d的依赖转化为对N的依赖,但是计算Q时$q_{n, m}=y_ny_mz_n^Tz_m$,仍然需要d。所以提出了Kernel来进行转换。
由于z特征是由x特征转换过来的,即:
\[z_n^Tz_m = \Phi(x_n)^T\Phi(x_m)\]这个过程是首先进行转换,然后再进行计算内积。如果我们将这个过程逆过来,那么就可以从对z域的d转换为对x域中的d的依赖。(因为进行特征转换多项式d一定会增加)。
以二次多项式为例,我们会得到如下所示,其中包含$x_0=1$和二次项$x_1x_2$和$x_2x_1$:

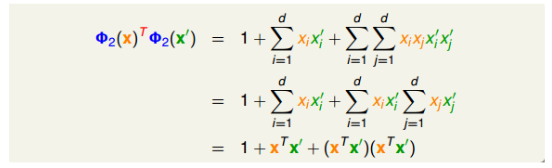
把这种合并特征转换和计算内积这两个步骤的操作叫做Kernel Function,用大写字母K表示。
例如上图就是:
\[K_{\Phi} = \Phi(x)^T\Phi(x{'}) = 1+(x^Tx^{'})+(x^Tx^{'})^2\]这样显然我们计算$q_{n,m}$时,仅仅与x域有关。
\[q_{n,m} = y_ny_mz_n^Tz_m=y_ny_mK(x_n,x_m)\]这样我们在dual SVM中所进行的全部可以进行转换

这个过程中,我们没有使用z空间做内积,即与z无关,这个过程称为kernel trick。引入kernel之后,大大提高了计算速度,这时,我们的算法过程就变为了:


Polynomial Kernel
除了上述的二次多项式,还可以进行扩充,比如带有系数,或者更高次项。
例如,带有相应系数,一般常见的有以下几种,其中最常使用的是第三种。

上述绿色多项式可以看成是一种完全平方公式

对于其中的$\gamma$,不同的选择对最终结果的影响是很大的,
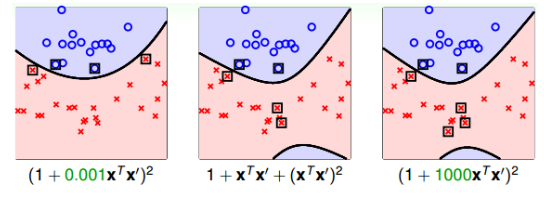
从而,我们最终推论我们的多项式表示,并同时引入$\zeta\ge0$和$\gamma>0$。

其中一共三个参数,通过选择不同的参数来获得不同的结果,一般从Q=1开始选择,当Q=1时,也就是前文的linear SVM。这是机器学习中的一大原则,即Occam’s Razor。
Gaussian Kernel
如果转换后的Z域是无限维的,为了解决这种问题,就提出了Gaussian Kernel
首先构造一个Kernel Function: $K(x, x^{‘})=e^{-(x-x^{‘})^2}$。然后利用反推,使用泰勒展开:

为了将$K(x, x^{‘})$定义为$\Phi(x)^T\Phi(x^{‘})$,那么我们就令$\Phi(x)$为:
\[\Phi(x) = e^{-x^2}(1, \sqrt{\frac{2}{1!}}x, \sqrt{\frac{2^2}{2!}x^2, }....)\]通过反推,我们得到了$\Phi(x)$,且$\Phi(x)$是无限维的,但是可以当作特征转换的函数,而这样的$Phi(x)$得到的核函数就是Gaussian kernel。
更一般的,对于原空间不为一维的情况(d>1),就引入缩放因子$\gamma>0$。因此,她对应的Gaussian kernel表达式为:
\[K(x, x^{'}) = e^{-\gamma\Vert z-z^{'}\Vert^2}\]那么我们的分类器就是,其中他是有n个高斯线性组合而成,其中n是SV的个数。并且每个高斯函数的中心都是对应的SV。通常也把高斯核函数成为经向基函数(RBF):

同样,我们需要注意$\gamma$的取值,不同的$\gamma$会得到不同的结果,如果太大,我们会得到过拟合的结果。
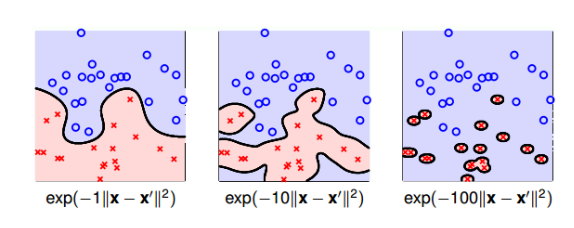
Comparison of Kernels
不同的核适用于不同的场景,对于简单的三种核,Linear Kernel和Polynomial Kernel还有Gaussian Kernel。
其中Linear Kernel的优点是计算简单、快速,可以直接使用快速得到参数值,而且从视觉上分类效果非常直观,便于理解;缺点是不能处理非线性问题
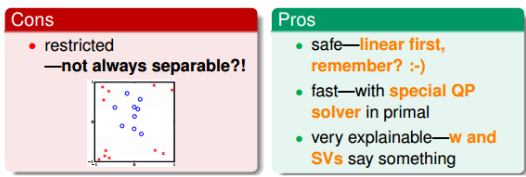
Polynomial Kernel则是阶数Q可以灵活设置,相比linear kernel限制更少,更贴近实际样本分布; 缺点是当Q很大时,K的数值范围波动很大,而且参数个数较多,难以选择合适的值。
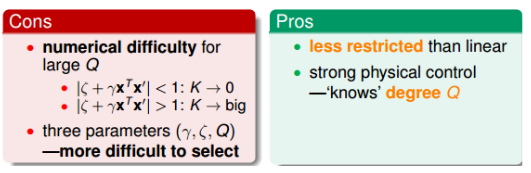
Gaussian Kernel的优点是边界更加复杂多样,能最准确地区分数据样本,数值计算K值波动较小,而 且只有一个参数,容易选择;缺点是由于特征转换到无限维度中,w没有求解出来,计算速度要低于 linear kernel,而且可能会发生过拟合。
Soft-Margin SVM
即使是SVM也会存在过拟合的问题,原因有两种,一种是SVM模型(Kernel)过复杂,另一种是由于我们坚持将所有的样本都分类正确,即不允许错误存在。但是在实际中,样本是存在noise的,因此,我们需要一定对噪声的容忍度

为了避免过拟合,我们就允许出现错误的点,并且将这些点当作noise,我们将这些noise放弃,但尽量让他们的个数越少越好。
为了引入允许犯错误的点,对Hard-Margin SVM的目标和条件进行修正,对于条件即我们仅考虑正确的点,让他们满足分类模型,但是对于错误的点,我们不进行设置。对于目标,我们同时加上错误点的个数,尽量使其变小。
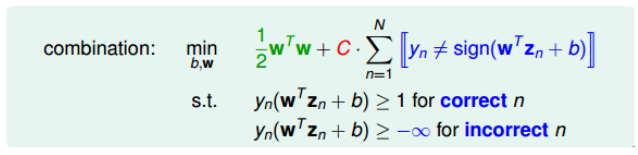
其中C参数是为了引入权衡目标第一项和第二项的关系,即权衡large margin和noise toleration。
但是他仍然不够完善,我们首先将两个条件进行合并(如果分类错误则大于1-$\infty$, 否则大于1)

无法进行计算,因为其中最小化目标中的第二项是非线性的,不满足二次规划(QP)的条件。所以。我们更换条件,将错误点的个数换成错误的程度(离边界越远,说明错误程度越大),。

修正后的表达式中,我们引入了新的参数$\xi_n$来表示每个点的犯错误的程度。
现在我们的最终目标就变为了:
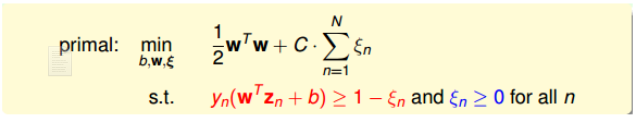
其中,$\xi_n$表示每个点的犯错程度,$\xi_n=0$表示没有犯错,$\xi_n$越大表示犯错程度越大。参数C表示large margin和noise toleration的权衡,边界越宽可能错误越多,大C表示希望得到更少的分类错误,意味着可能边界更窄,而小C希望得到更宽的边界,则可能导致分类错误增加。
使用QP求解时,引入引入$\xi$,所以增加了N个参数即参数个数为$d+1+N$,限制条件加了$\xi_n>0$,则条件总数为2N。

Sovling Soft-Margin SVM
为了便于使用kernel求解,我们同样为他增加了拉格朗日因子$\alpha_n$和$\beta_n$。其形式为:

与Dual SVM同样的转换,我们会得到
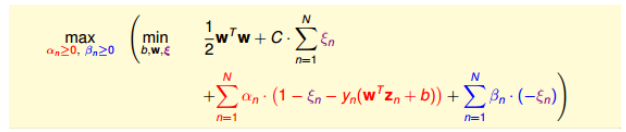
然后消去里面的min
\[\frac{\partial L}{\partial \xi_n} = 0 = C-\alpha_n-\beta_n \\ \frac{\partial L}{\partial b}=0=-\sum_{n=1}^N\alpha_ny_n \\ \frac{\partial L}{\partial w}=0=w-\sum_{n=1}^N\alpha_ny_nz_n\]然后同样将其转换为最小化形式可以得到,我们的最终目标变为了:
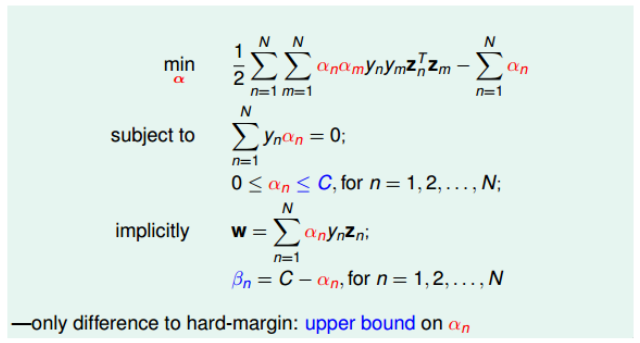
可以看出来,与Hard-Margin SVM的区别仅仅只是一些条件不同,我们对$\alpha_n$增加了限定条件即$\alpha_n \le C$。且出现了新的拉格朗日因此$\beta_n = C-\alpha_n$。也因此条件增加了N个($\alpha$的上界条件)
我们的KKT条件就成为了:
- $all \ 0\le\alpha_n\le C$
- $\sum_{n=1}^N\alpha_ny_n=0$
- $w=\sum_{n=1}^N\alpha_ny_nz_n$
之后,我们就可以使用二次规划的相应解法来计算最终结果了。

最关键的问题在于b的值,在hard-margin SVM中,我们是找到了SV,然后代入计算就可以了,但是在soft-margin SVM由于增加了$\alpha$和$\xi$两个拉格朗日因子。因此,相应的complementary slackness条件有两个:
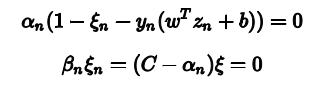
首先找到SV,即$\alpha_s>0$的点,然后根据第二个条件,如果$C\neq\alpha_n$,则一定有$\xi_n$等于0,然后带入第一个式子就可以求出b的最终表达式,为此,我们把$0<\alpha_n<C$的点称为free SV。所以引入核函数的最终结果为(两边同时乘以$y_n$): \(b = y_s-\sum_{SV}\alpha_ny_nK(x_n, x_s)\)
尽管上述$\alpha_n\neq C$是假设的,但是一般情况下至少存在一组SV使得$\alpha_n<C$的概率是很大的。如果没有出现free SV的情况,那么b通常会有许多不等式条件限定,值是不确定,只要找到一个满足KKT条件的任意一个b值即可。
Model Selection
Soft-Margin中有三个参数,其中C是权衡宽度和噪声容忍度的。不同的C意味着不同的模型,如果C过大,依然会出现过拟合的现象:
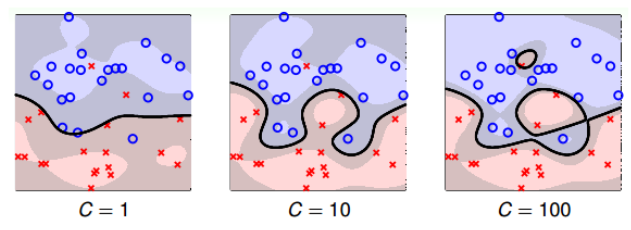
而对于不同的$\alpha_n$的值,已知$0 \le \alpha_n \le C$满足两个相应的complementary slackness条件:
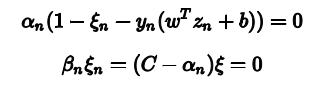
所以如果$\alpha_n =0$,得到$\xi_n=0$。$\xi_n=0$,则表示该点没有犯错,$\alpha_n=0$表示该点不是SV。所以对应的点在margin之外(或者margin上)。且分类正确。
如果$0<\alpha<C$,得到$\xi_n=0$,且$y_n(w^Tz_n+b)=1$。$\xi_n$表示该点没有犯错,$y_n(w^Tz_n+b)=1$表示了该点在margin上,即这些点为free SV。
如果$\alpha_n=C$,不确定$\xi_n$是否为零,只能得到$1-y_n(w^Tz_n+b)<\xi_n$。这表示该点偏离margin的程度,$\xi_n$越大表示偏离越大。只有$\xi_n=0$时,该点在margin上,所以这种情况对应的是点在margin之内负方向,有分类正确的也有分类错误的。这些点被称为bounded SV。

对于这些参数的选择,我们仍然可以通过前面讲的validation。
最常见的就是V-Fold cross validation。将不同的(C, $\gamma$ )组合得到不同的$E_{cv}$。然后选择其中最小的一个。我们也使用Leave-One-Out CV。

由于对于SVM问题,他的验证集Error满足:
\[E_{loocv}\le \frac{SV}{N}\]这是因为我们的SVM分类器仅w = \sum_{n=1}^N\alpha_ny_nz_n
\beta_n = C-\alpha_仅只跟SV有关的。所以,我们可以通过选择SV数量来选择我们的参数,一般来讲,SV越多,说明模型越复杂,越可能造成过拟合。通常都是选择SV数量较少的模型。
所以,我们通常先选择SV数量较少的模型,然后再使用cross-validation。
总结
为了提高对噪声的容忍度,我们提出了一种大间隔的分类器,并且从最简单的线性可分扩展到非线性问题,同时为了提高对非线性问题的处理速度,我们提出了核函数这一概念,它可大大提高我们的运算速度。
\[Polynomial\ Kernel: K(x, x^{'}) = (\zeta+\gamma x^Tx^{'})^Q \\ Gaussian\ Kernel: K(x, x^{'}) = exp(-\gamma \Vert x-x^{'}\Vert^2)\]为了保证不过拟合,增加了对错误节点的容忍度,从而产生了Soft-Margin SVM,在日常实践中,应当尽量选择Soft-Margin SVM模型。他的模型为:
\[\begin{align*} \min_\alpha \quad& \frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\alpha_n\alpha_my_ny_mK(x_n, x_m)-\sum_{n=1}^{N}\alpha_n\\ s.t. \quad & \sum_{n=1}^{N}y_n\alpha_n = 0\\ &0 \le \alpha_n\le C \quad for\ n=1, 2, 3.....N; \end{align*}\]根据上式我们使用求解二次规划的方法进行求解,然后我们就可以得到我们的$\alpha$,然后我们就可以求出w和b。
\[w = \sum_{n=1}^{N}\alpha_ny_nz_n\\\]对于求解b,我们有complementary slackness条件
\[\begin{align*} & \alpha_n(1-\xi_n-y_n(w^Tz_n+b)) = 0\\ &\beta_n\xi_n=(C-\alpha_n)\xi = 0 \end{align*}\]来求解w和b。
\[\begin{align*} & w = \sum_{n=1}^{N}\alpha_ny_nz_n\\ & b = y_s-\sum_{n=1}^{N}\alpha_ny_nK(x_n, x_s) \end{align*}\]对于求解式中$\alpha$,显然可以看出w和b的值仅仅跟$\alpha_n>0$的值有关,我们就称这些点为SV。在Soft-Margin SVM中由于引入了新的变量$\xi$。所以,进一步细分我们将:
- $\alpha_n=0$, $\xi_n=0$的点是分类正确,且在margin之外的点
- $0<\alpha<C$, $\xi_n=0$的点是没有犯错,但是在margin上的点,即free SV。
- $\alpha=C$,$\xi_n$不确定的点,这表示偏离margin的点,$\xi$越大偏离越大,有分类正确也有错误的点。即bounded SV.
标注:对于SVM的求解,可以使用序列最小优化算法(SMO)。