机器学习(9)-序列最小优化算法

序列最小优化算法(Sequential minimal optimization, SMO)是一种用于解决支持向量机(SVM)训练过程中所产生优化问题的算法。在前文中，我们是使用二次规划工具来求解SVM，SMO算法则提供了另一种思路。

SVM

我们已经了解了SVM的的目标函数即:

\[\begin{align*} \min_\alpha \quad \Psi(\alpha)= & \frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\alpha_n\alpha_my_ny_mK(x_n, x_m)-\sum_{n=1}^{N}\alpha_n\\ s.t. \quad & \sum_{n=1}^{N}y_n\alpha_n = 0\\ &0 \le \alpha_n\le C \quad for\ n=1, 2, 3.....N; \end{align*}\]

也因此，我们只需要得到$\alpha$就可以通过条件获得我们的w和b。

SMO

由于SVM中存在限制条件$\sum_{i=1}^{n}y_i\alpha_i=0$，因此在我们更新$\alpha$时，我们必须要考虑限制条件，在实际操作中是十分麻烦的。

而SMO算法采用每次只更新两个变量的思想，从而避免了这一限制。我们假设算法在某次更新中更新的变量为$\alpha_1$和$\alpha_2$，而将其他的变量设置为常量。

前提条件是标签$y\in{-1, 1}$。那么显然$y^2=1$

那么我们的$\Psi$就变成了仅跟$\alpha_1$和$\alpha_2$的函数，而其他内容则为常数:

\[\begin{align} \Psi(\alpha_1, \alpha_2) =& \frac{1}{2}\alpha_1^2K_{1, 1}+\frac{1}{2}\alpha_2^2K_{2, 2}+\alpha_1\alpha_2y_1y_2K_{1, 2}+\\&y_1\alpha_1\sum_{n=3}^{N}\alpha_ny_nK_{n, 1}+y_2\alpha_2\sum_{n=3}^N\alpha_ny_nK_{n, 2}-\alpha_1-\alpha_2-Content\\ =& \frac{1}{2}\alpha_1^2K_{1, 1}+\frac{1}{2}\alpha_2^2K_{2, 2}+\alpha_1\alpha_2y_1y_2K_{1, 2}+y_1\alpha_1v_1+y_2\alpha_2v_2-\alpha_1-\alpha_2-Content\\ & \text{为了便于计算，另}v_1=\sum_{n=3}^N\alpha_ny_nK_{n, 1}, v_2=\sum_{n=3}^N\alpha_ny_nK_{n, 2} \end{align}\]

直接求两个变量仍然不够简单，由于限制条件的存在，我们可以将$\alpha_1$和$\alpha_2$建立关系式，然后首先求出一个变量，再求出另外一个变量。

\[\begin{align*} \sum_{n=1}^{N}\alpha_ny_n=0 & \Rightarrow \alpha_1y_1+\alpha_2y_2=-\sum_{n=3}^N\alpha_ny_n=\zeta\\ &\stackrel{两边×y_1}{\Longrightarrow} \alpha_1 = \zeta y_1 - \alpha_2y_1y_2 \end{align*}\]

然后将上述内容带入$\Psi$中，可以得到:

\[\begin{align*} \Psi(\alpha_2) =& \frac{1}{2}(\zeta y_1-\alpha_2y_1y_2)^2K_{1, 1}+ \frac{1}{2}\alpha_2^2K_{2, 2}+(\zeta y_1-\alpha_2y_1y_2)\alpha_2y_1y_2K_{1, 2}\\ &+(\zeta y_1 - \alpha_2y_1y_2)y_1v_1+y_2\alpha_2v_2-(\zeta y_1-\alpha_2y_1y_2)-\alpha_2+Content\\ = &(\frac{1}{2}K_{1, 1}-K_{1, 2}+\frac{1}{2}K_{2, 2})\alpha_2^2+(-\zeta y_2K_{1,1}+\zeta y_2K_{1, 2}-v_1y_2+y_2v_2+y_1y_2-1)\alpha_2\\ &+\zeta v_1+\frac{1}{2}\zeta^2K_{1, 1}-\zeta y_1+Content \end{align*}\]

这是一个二次函数，并且他是一个凸函数，也就是说，这是一个凸优化问题，那么我们对其求梯度并置为0。

\[\frac{\partial\Psi(\alpha_2)}{\partial \alpha_2} = (K_{1, 1}+K_{2, 2}-2K_{1, 2})\alpha_2-\zeta y_2K_{1, 1}+\zeta y_2K_{1, 2}-v_1y_2+y_2v_2+y_2y_1-1=0\]

显然，上述解出来的$\alpha_2$就是我们想要的结果，我们将其称为$\alpha_2^{new}$。

我们希望能够将求解进行简化。希望它能够想梯度下降法一样可以通过上一步中的解$\alpha_2^{old}$来得到新的答案。

为此，我们假设$f(x) =w^Tx+b= \sum\limits_{i=1}^N\alpha_iy_iK(x_i, x)+b$

对于对于求解过程中的v1和v2可以用已知的$\alpha^{old}$ 表示为:

\[\begin{align} v_1 = &\sum_{n=3}^N\alpha^{old}_ny_nK_{n, 1} = f(x_1)-\alpha^{old}_1y_1K_{1, 1}-\alpha^{old}_2y_2K_{1, 2} - b\\ v_2 = &\sum_{n=3}^N\alpha^{old}_ny_nK_{n, 2} = f(x_2)-\alpha^{old}_1y_1K_{1, 2}-\alpha^{old}_2y_2K_{2, 2} - b\\ v_2-v_1= & f(x_2)-f(x_1)+\alpha^{old}_1y_1(K_{1, 1}-K_{1, 2})+\alpha^{old}_2y_2(K_{1, 2}-{K_{2, 2}})\\ =&f(x_2)-f(x_1)+\zeta K_{1, 1}-\zeta K_{1, 2}+\alpha^{old}_2y_2(2K_{1, 2}-K_{2, 2}-K_{1, 1}) \end{align}\]

将这个式子代入上式中可以得到(将1换为$y_2^2$):

\[\begin{align} \frac{\partial\Psi(\alpha_2)}{\partial \alpha_2} = &(K_{1, 1}+K_{2, 2}-2K_{1, 2})\alpha^{new}_2-(K_{1, 1}+K_{2, 2}-2K_{1, 2})\alpha_2^{old} \\&+y_2(f(x_2)-f(x_1)+y_1-y_2) \end{align}\]

其中$f(x)-y$就是预测值与真实值的误差，将其设为$E_i$，同时为了方便计算，我们也另$\eta = K_{1, 1}+K_{2, 2}-2K_{1, 2}$。那么最终结果就变为了:

\[\eta \alpha_2^{new}-\eta\alpha_2^{old}+y_2(E_2-E_1) = 0\]

变换可得:

\[\alpha_2^{new} = \alpha_2^{old} - \frac{y_2(E_2-E_1)}{\eta}\]

约束条件

我们已经知道了SMO中更新$\alpha_2$的过程，但是在SVM中，我们的$\alpha_2$是有约束的:

\[\begin{align} & y_1\alpha_1^{new}+y_2\alpha_2^{new} = y_1\alpha_1^{old}+y_2\alpha_2^{old} = -\sum_{n=3}^N\alpha_ny_n=\zeta\\ & 0 \le\alpha_n\le C \end{align}\]

我们将1式两边同时乘以$y_2$，那么我们可以得到

\[\alpha_2 = \zeta - y_1y_2\alpha_1\]

所以一共有四种可能，分别是

$y_1\neq y_2, \zeta \ge 0$
$y_1\neq y_2, \zeta<0$
$y_1 = y_2, \zeta \ge 0$
$y_1=y_2, \zeta <0$

我们分别对这四种情况做出曲线，可以得到

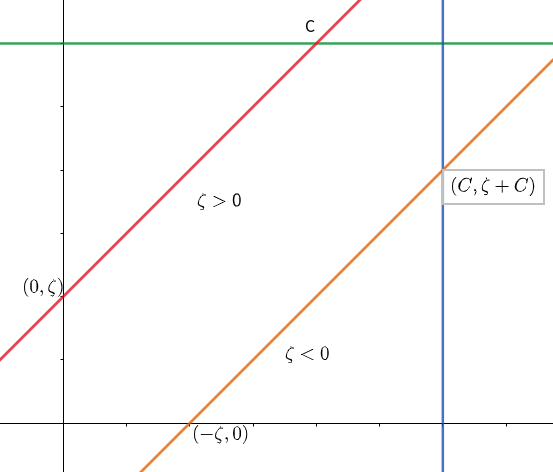
当$y_1\neq y_2$时，斜率为正，所以如图得到两个条件:

$\zeta \ge0： \zeta \le\alpha_2 \le C$
$\zeta <0: 0 \le \alpha_2 \le \zeta+C$

经过整理，我们可以得到

\[\max(\zeta, 0) \le \alpha_2 \le min(C, \zeta+C)\]

同理，当$y_1=y_2$时，斜率为负，此时$\zeta<0$不会出现在方格中，但是此时需要考虑$\zeta$和C的关系.如图:

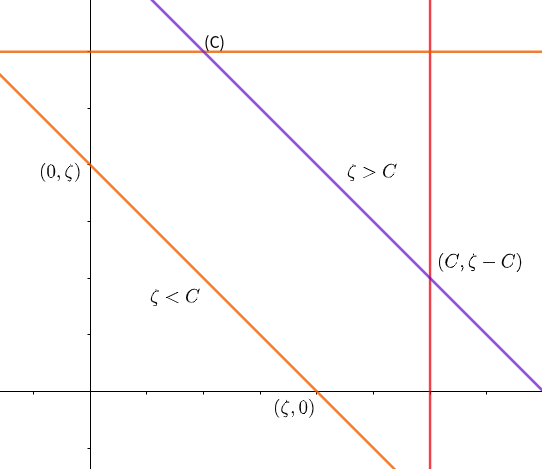
$\zeta > C, \zeta-C \le \alpha_2 \le C$
$\zeta < C, 0\le \alpha_2 \le \zeta$

经过整理我们得到:

\[\max(0, \zeta-C) \le \min(C, \zeta)\]

综上，我们得到了对于一个新的$\alpha_2^{new} $:

当$y_1\neq y_2$时，$\alpha_2-\alpha_1=\zeta$:
- 下届$L = max(0, \alpha_2^{old}-\alpha_1^{old})$
- 上界$H = min(C, C+\alpha_2^{old}-\alpha_1^{old})$
当$y_1=y_2$时，$\alpha_1+\alpha_2=\zeta$：
- 下届$L = max(0, \alpha_2^{old}+\alpha_1^{old}-C)$
- 上界$H = min(C, \alpha_2^{old}+\alpha_1^{old})$

所以，经过约束后的$\alpha^{new, clipped}_2$就等于:

\[\alpha^{new, clipped}_2 = \left \{\begin{matrix} H & \alpha_2^{new} > H\\ \alpha_2^{new}& L\le \alpha_2^{new}\le H\\ L& \alpha_2^{new}<L \end{matrix}\right.\]

而对于$\alpha_1$：

\[\alpha_2 = \zeta - y_1y_2\alpha_1\]

$\alpha_1$和$\alpha_2$的启发式选择方法

在SVM中，我们提到对于Soft-Margin SVM中，$\alpha$的取值对应于不同的样本的位置:

$\alpha_n=0$时，表示样本正确分类，且是在Margin之外，即$y_nf(x_n)\ge 1$
$0 < \alpha_n < C$时，表示样本是支持向量，在Margin之上，即$y_nf(x_n) = 1$
$\alpha_n=C$时，表示在Margin之内，即$y_nf(x_n)\le1$

那么相反，如果

$y_nf(x_n)\ge 1$, 那么就一定有$\alpha_n=0$，而$\alpha_n>0$是不满足的
$y_nf(x_n)=1$，那么一定有$0<\alpha_n<C$，而$\alpha_n=0$和$\alpha_n=C$都是不满足的
$y_nf(x_n)\le 1$，那么一定有$\alpha_n=C$，而$\alpha_n< C$是不满足的。

所以我们在更新时就需要更新这些节点。

那么第一步就是找到一个不满足的$\alpha_1$，这是因为Osuna定理证明了只要选择出来的两个$\alpha_i$有一个违背了KKT条件，那么目标函数就会减少。

而选择一个$\alpha_1$之后，第二个$\alpha_2$，我们应当选择满足$\max\vert E_1-E_2\vert$的样本点。

w和b的更新

在SVM中，我们已经知道了

\[w = \sum_{i=0}^{N}\alpha_ny_nz_n\\ \alpha_n(1-\xi_n-y_n(w^Tz_n+b)) = 0\\ \beta_n\xi_n = (C-\alpha_n)\xi =0\]

所以当$0<\alpha_1^{new} <C$时, $\xi=0$,此时我们的$b_1^{new}$就等于:

\[\begin{align} b_1^{new}& = y_1 - \sum_{n=1}^N\alpha_ny_nK(x_n, x_1)\\ &= y_1 - \sum_{n=3}^N\alpha_ny_nK_{i, 1}-\alpha_1^{new}y_1K_{1,1}-\alpha_2^{new}y_2K_{1, 2}\\ &=y_1-v_1-\alpha_1^{new}y_1K_{1,1}-\alpha_2^{new}y_2K_{1, 2}\\ &=b^{old}-E_1-y_1(\alpha_1^{new}-\alpha_1^{old})K_{1, 1}-y_2(\alpha_2^{new}-\alpha_2^{old})K_{1, 2} \end{align}\]

同理$b_2^{new}$为:

\[=b^{old}-E_2-y_1(\alpha_1^{new}-\alpha_1^{old})K_{1, 2}-y_2(\alpha_2^{new}-\alpha_2^{old})K_{2, 2}\]

所以，我们对b的更新有如下规则:

\[b^{new} = \left \{\begin{matrix} b_1^{new} & \text{if} \ 0< \alpha_1^{new}< C\\ b_2^{new} & \text{if} \ 0< \alpha_2^{new}< C\\ \frac{b_1+b_2}{2}& \text{otherwise} \end{matrix}\right.\]

总结

对于SVM，我们有目标为：

通常使用SMO算法对其进行更新。

其算法过称为：

while{

使用启发式方法选取一对$\alpha_1$和$\alpha_2$。
固定其他参数，更新$\alpha_1$和$\alpha_2$。
更新w和b，然后重新进行。

}