SIFT算法
尺度空间
在现实世界中,由于物体观察的远近不同,虽然人眼观察的有所差别,但是依旧可以分辨出同一样东西,这就是尺度不变性.如果想要让计算机实现这一功能,就需要为计算机提供不同尺度下的物品让其学习.
站在巨人的肩膀上大奥特曼打小怪兽
多分辨率图像金字塔
图像金字塔是早期图像多尺度的表现形式,通常是同一图像在不同的分辨率下的一组结果.其生成过程包括两个部分
- 高斯预滤波, 对原始图像平滑
- 对图像处理后进行降采样(一般是频率为2,即长宽为原图像的1/2),之后重复1,2过程.
但是对于多分辨率高斯金字塔其本质还是降维采样,其局部特征依旧难以保持,即难以保持尺度不变性.
高斯尺度空间
高斯尺度空间从原理上就是通过模糊图像来模拟人在不同距离观察物体的情况.距离物体越远则越模糊,越近就越清晰.使用不同的参数模糊图形(保持分辨率不变),是尺度空间的另一种表现形式.
一般我们会使用高斯函数来模糊图像,这也是被成为高斯尺度空间的理由.
对于高斯核函数(二维高斯函数)的公式:
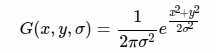
其中σ就被称为尺度空间因子.因为他反映了图像被模糊的程度,其值越大图像越模糊.
通过高斯模糊,我们就可以得到一幅图片的一个高斯尺度空间.
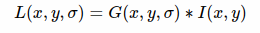
## SIFT的过程
- 尺度空间的极值点检测: 通过DoG来检测对尺度和选择不变的兴趣点
- 特征点的定位: 寻找稳定的特征点
- 特征方向的赋值: 保证旋转不变性
- 特征点描述符: 为图像匹配建立独一无二的描述符
尺度空间的极值点检测
相关研究
在2002年,Mikolajczyk(An affine invariant interest point detector)提出高斯拉普拉斯算子(Log)可以用于检测出比较好的尺度不变性的特征点.
在1994年,Lindeberg(Scale-space theory: A basic tool for analysing structures at different scales)提出差分高斯函数(Dog)与高斯拉普拉斯算子相似.而且运算量会降低很多.
本文就是使用高斯差分函数(DoG)来检测尺度不变的特征值
DoG的定义
对于高斯差分函数,两个相邻的高斯空间的图像相减就得到了DoG的响应图像.也就是说DoG的数学定义为:
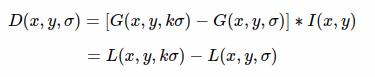
其中L(x, y, σ)是图像的高斯尺度空间,而k是相邻的两个高斯尺度空间的比例因子
在求出的值后,DoG的尺度应该是减数的尺度.(这是因为提出了(k-1),而k-1被当做常数,对特征点检测没有影响)
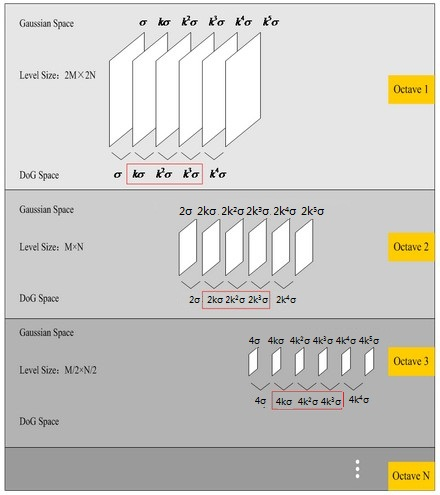
高斯金字塔的构造
为了得到DoG的图片,我们就要首先构造高斯尺度空间.
在构造尺度空间时,SIFT在降维采样点基础上加上高斯滤波实现.如图左侧剽窃自大奥特曼打小怪兽:
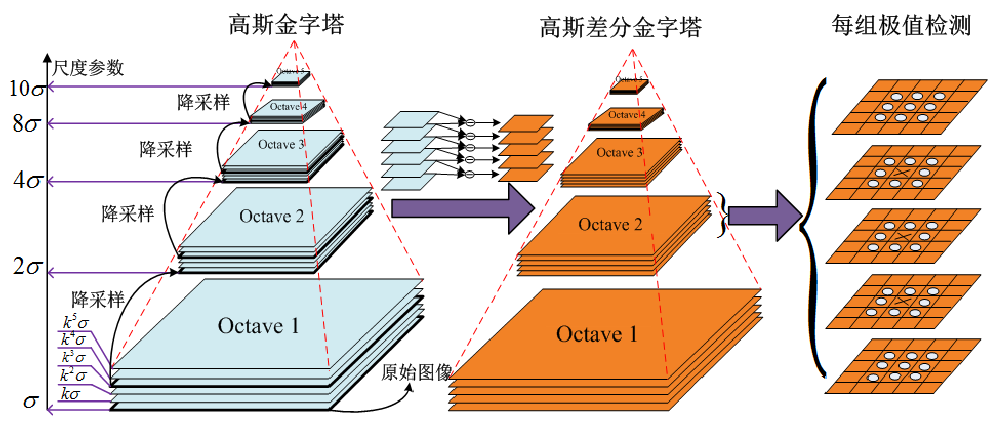
可知,高斯金字塔有多组,且每组有多层.其中的参数:
-
O: 组数(我没有在论文中看到对组数的讨论,所以参考博客) 一般组数(m为行数,n为列数)为
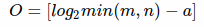
- S: 每组层数: 我不大理解这个定义,高斯金字塔中每组有S+3层图片
-
k: 相邻高斯尺度的比例因子:其值设为
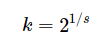
- σ: 初始尺度.
得到上述参数后,我们就可以构建尺度空间 (在论文中,S=3, σ=1.6)
- 第0组:我们首先将原图扩大两倍作为起始图像I0,然后对他进行高斯模糊I0∗G(x,y,σ0)作为第0层,第1层就是I0∗G(x,y,k²σ0),第2层就是I0∗G(x,y,k³σ0)…以此类推,一直到S+3层
- 第一组: 选择上一组中尺度为2¹σ0的尺度图像,然后将其降采样作为这一组的第0层,然后进行高斯模糊构建高斯金字塔
- 第二组: 选择上一组中尺度为2²σ0的尺度图像,然后将其降采样作为这一组的第0层,然后类推
- 第O层: 同样选择上一组中尺度为(2^o)σ0的尺度图像,然后类推即可。
事例就参考blog, 因为我真的写不出LaTex,就很难看.
注意:
-
我们在创建高斯金字塔时,第0组第0层是原图像的二倍,这是因为可以更加充分的提取特征点.
-
在实际应用中,我们的高斯金字塔一共生成了S+3个图像
-
每一组的初始图像的尺度都是上一组的初始图像的尺度的二倍。
特征值检测
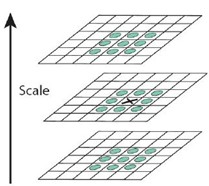
为了寻找DoG金字塔尺度空间的极值点,每个像素点要和其图像域(相同大小的图像)和尺度域(相邻的尺度空间)的所有相邻点进行比较,当其大于(或者小于)所有相邻点时,该点就是极值点,即被保留。如图所示,中间的检测点要和其所在图像的3×3邻域8个像素点,以及其相邻的上下两层3×3邻域18个像素点,共26个像素点进行比较。
#### 尺度变化的连续性
对于S的定义我实在是没有一个准确的定义,而论文中给的又让人有些难以理解。
部分博客是认为为尺度变换的连续性,虽然在某些原理上站得住脚,但是连续性我认为更多的是通过设置每一组的初始图像来保持的(也就是初始的尺度设置为上一层初始尺度的二倍)。而S是通过DoG金字塔中获取特征点的层数。这是一个实验值。在论文中,当S为3时,检测特征点最佳。
比如如果要得到S层图像,那么DoG金字塔就需要S+2层,而高斯金字塔就需要S+3层。
比如设置S为3,高斯金字塔为6, DoG金字塔为5,然后我们在求局部最大值时,没一组只需要比较三层。
特征点的定位
在上一个过程中只是检测出特征点的候选点,之后就要删除一些不好的极值点。
删除的不好的极值点,主要有两种: 低对比度的特征点,不稳定的边缘响应点
低对比度的特征点
我们在尺度空间为σ的尺度图像中检测到一个局部极值点。那点的空间位置就是(x, y, σ)。并设其极值点偏移量为Δx。
为了判断它是否为低对比度的特征值,我们首先将尺度空间方程D(x,y,σ)使用了泰勒级数展开(到二阶)变换。
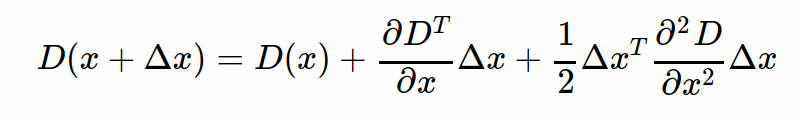
对Δx求导并让方程等于零,可以得到极值点的偏移量为:
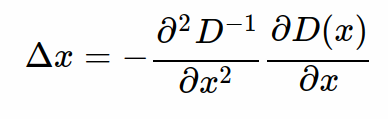
然后再把求得的Δx带入到D(x)的泰勒展开式中:
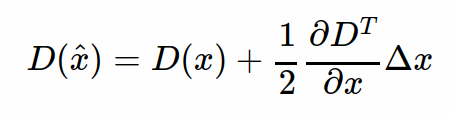
其中x^=x+Δx,设对比度的阈值为T,对比度为D(x^)的绝对值|D(x^)|,若|D(x^)|≥T,则该特征点保留,否则剔除掉。
在论文中,D(x^)小于0.03的都要被排除(设像素值在[0, 1]范围内)
不稳定的边缘响应点
对于删除不稳定的边缘响应点使用的是Harris角点检测那一套
我们通过求H矩阵(这里没有对H矩阵进行高斯卷积),然后求Harris角点即可,然后进行判断
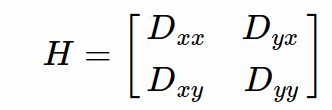
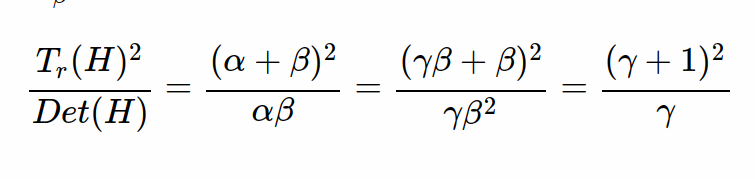
如果所求的Harris角点是Tr(H)²/Det(H), 如果其大于某一阈值时,则抛弃,否则保留。
而在此处阈值设置为, 其中Tr在论文中取Tr=10。
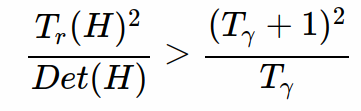
特征方向的赋值
这一过程主要是为了实现图像的旋转不变性
对于图像中某一点的方向,我们可以通过梯度方向近似表示即:
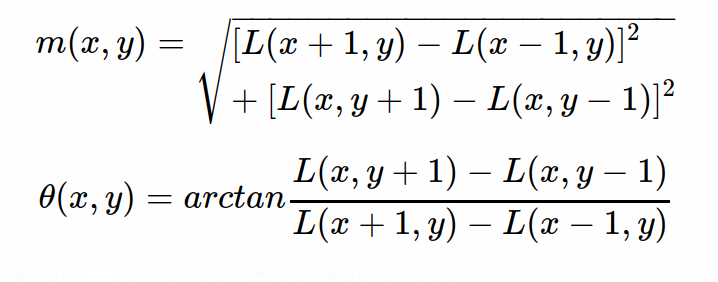
而在SIFT中描述特征点的方向时,我们并不仅仅只是求关键点的方向,而是通过一个一个以该特征点尺度σ的1.5倍为半径,以特征点为圆心的窗口来决定。我们为这个区域中每一个点求梯度。
之后,我们建立一个方向直方图。直方图的横轴就是方向的角度。在论文中这个直方图有36个柱子,即每10度一个柱子。纵轴就是方向对应梯度幅值的累加。而直方图的峰值就是特征点的主方向。
在梯度直方图中,当存在一个主峰值80%的柱值时,他也会被认为是该特征点的辅助方向。这也意味着,一个特征值可以检测到多个方向(即一个特征值可以产生多个坐标、尺度相同,但是方向不同的特征点)
似乎我们还可以通过抛物线差值来提高精度。。。放过我吧