迄今为止, 我们已经学了角点检测到图像匹配, 再到图像配准整个过程, 现在,我们已经可以学习,如何将两个或多个图像合成全景图。

从公共平面开始
我们在了解相机的工作原理时,我们知道,从3D图像到2D图像,是通过射线投影得到的,如果我们将所有图像都投影到同一个平面上,显然,我们可以进行图像的拼接。
基本流程就是:
- 从同一位置拍摄一系列图像,即,围绕光心旋转相机
- 计算第二个图像与第一个图像之间的变换
- 计算第二个图像以与第一个图像部分重合
- 将两者融合在一起创建拼图
- 如果有更多图像,重复以上步骤
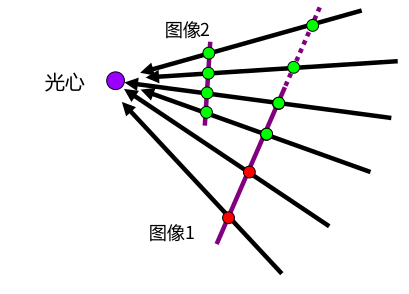
在图像配准时,我们使用最小二乘法求得单应矩阵,实际上根据上一讲的相机原理,我们对于单应矩阵该有了更深的理解。我们社图像一和图像二的参数如图:

所以,对于两个图片之间的变换有了如下过程
步骤 1:将图像2中的像素转换为相机2坐标系中的射线。
\[\begin{bmatrix}X_2 \\ Y_2\\ Z_2 \end{bmatrix} = K_{2}^{-1}\begin{bmatrix}x_2\\y_2\\ 1\end{bmatrix}\]步骤 2:将相机2坐标系中的射线转换为相机1坐标系中的射线。
\[\begin{bmatrix}X_1 \\ Y_1\\ Z_1 \end{bmatrix} = R_{2}^{T}K_{2}^{-1}\begin{bmatrix}x_2\\y_2\\ 1\end{bmatrix} , 其中 R_2^{-1} = R_2^{T}\]步骤 3:将相机1坐标系中的射线转换为图像1坐标中的像素。
\[\begin{bmatrix}x_1 \\ y_1\\1 \end{bmatrix} ~ K_1 R_{2}^{T}K_{2}^{-1}\begin{bmatrix}x_2\\y_2\\ 1\end{bmatrix} , 其中K_1R_2^TK_2^{-1}就是3*3的单应矩阵\]通过上述三个步骤,我们就可以将图像1融合到图像2平面上。虽然是有想应得融合算法即可得到融合图
全景
虽然上述投影到统一平面上十分简单,但是是无法实现全景图的,如果我们想要360度视野的话, 投影成球形再展开是一个更好的选择。
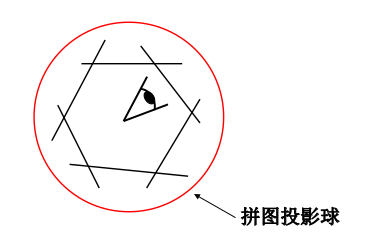
此时的成像,我们已经不是一个平面了,而是一个球体,其中,相机在球体的中心。我们保持光心不动,然后旋转,就可以得到一个球360度的图片,然后,我们将球体展开,就形成了全景图。
球面投影
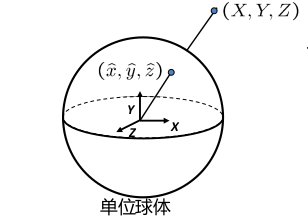
同样是在进行平面投影时的原理,我们将3D物体投影到球面上。
这个过程,我们有三个坐标系,即世界坐标系,相机坐标系(球面坐标系), 像面坐标系(球面图像坐标)。
首先将世界坐标系转换成相机坐标系,此时相机坐标系的原点在球的中心。
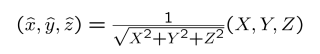
由于此时相机坐标时是一个3维的,为了表示变为平面坐标,我们新设立了两个变量$\theta$, $\phi$。
其中,$\theta$是射线与Y, Z平面的夹角, 顺时针为正。
$\phi$是射线与X, Z平面的夹角, 顺时针为负。
所以,我们就可以将球体的坐标转换为球面坐标
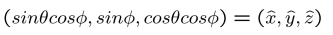
之后,我们就可以将球体展开,此时他的两个坐标分别为$\theta$和$\phi$
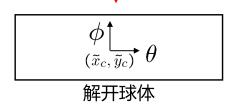
最后,我们就可以将球面坐标转化为球面图像坐标。
由于刚刚的球体是单位球体,所以,为了得到更好的图像表示,我们需要将其伸缩。通常情况下,我们使用半径为S的球体表示(S为相机焦距)。就如同平面成像一样,我们使用相似定律并加上平移即可得到最后的图像坐标。
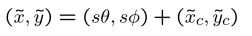
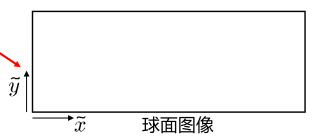
其中S对图像的影响如图:

我们已经知道通过球体坐标形成全景图的原理,之后,我们只需要对齐球面坐标即可,一下两幅图片是相机围绕垂直轴旋转了$\theta$角度形成的两个图片

为了将两者对齐,我们水平平移$\theta$角度即可,这意味着,我们可以通过平移来对其球面坐标。
装配全景图
在理想情况下,我们只需要将每一对拼接在一起,融合,人后裁剪即可

漂移
但是在实际应用中,虽然时间的推移积累了小错误,就产生了飘移现象
为了解决这种方法,我们一般有多种方式,最简单的是在末尾添加第一个图像的另一个副本,这就得到了一个约束,即$y_{n} = y_{1}$
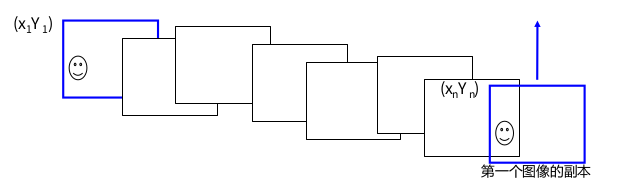
之后,我们可以通过多种方式
- 我们增加位移$(y_{1}-y_{n})/(n-1)$到第一个后面的每幅图像,即均向上平移
- 应用仿射卷扰: ${y}’ = y + ax$(不大懂)
- 求解一个大的优化问题,加入此约束, 这是最好的解决方法,但更复杂。
融合
由于亮度的不同或者一些其它问题,我们对于图像的融合并不会十分完美

为了无缝的融合在一起,我们需要一些算法,最为简单的就是羽化
羽化
我们对于两个图片的连接处,设置一个从0到1的渐变和一个从1到0的渐变
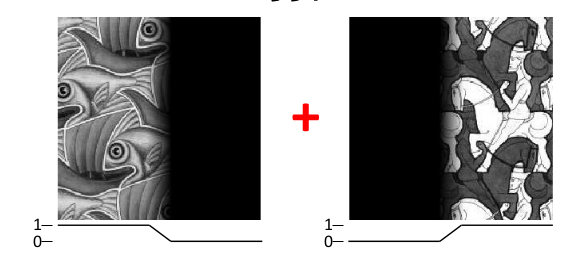
之后将两者融合, 我们只需要在渐变的区间内,将两者的像素值相加就可以了
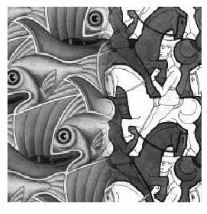
对于这种方法,我们需要选择一个恰当的渐变区间,不同的渐变区间对于融合的效果是不一样的
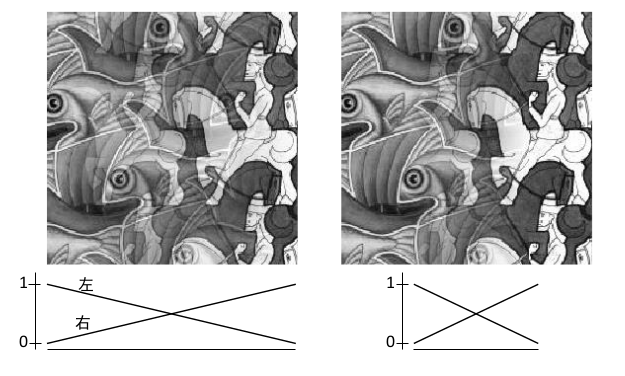
除此之外,我们还有金字塔混合和Alpha混合,在后面再说。看一下论文
去虚影
这个要看论文。。。