Wlgls 冲鸭!

第六节：计算机视觉 图像配准

2019-10-20
Computer_Vision

当我们进行图像的匹配之后，我们就可以进行图像的配准了，即，求解两个图像的变换矩阵，之后，我们甚至可以将两个图片合并。

2019-10-31-15-07-46.png

理论基础

在图像的变换和卷绕中，我们已经建立了一个图片经过变换成为另一个图片的过程，事实上，我们在进行图像配准的时候,就是给出了两个图像，让我们判断图像之间的变换关系的过程。

如果图像A经过一些变换能得到图像B，我们只需要计算出这组变换，就可以得到图像的配准，并进行拼接。

所以，寻找图片中与所有匹配项最符合的变换T就是图像配准的过程。

最简单的例子就是平移

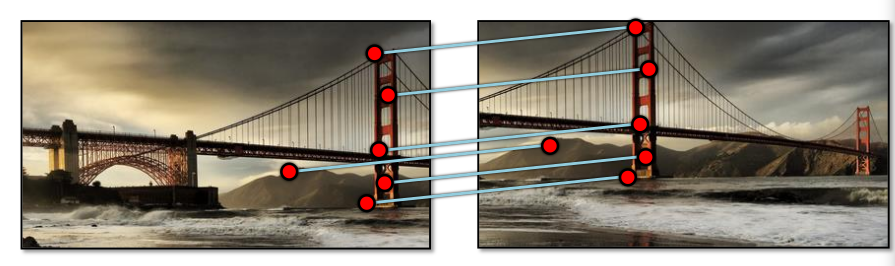
2019-10-31-15-39-37.png

很明显，图片B中的特征点就是图片A中特征点平移的来的。所以，只需要计算出平移量(xt, yt)，我们甚至可以将两个图像合成

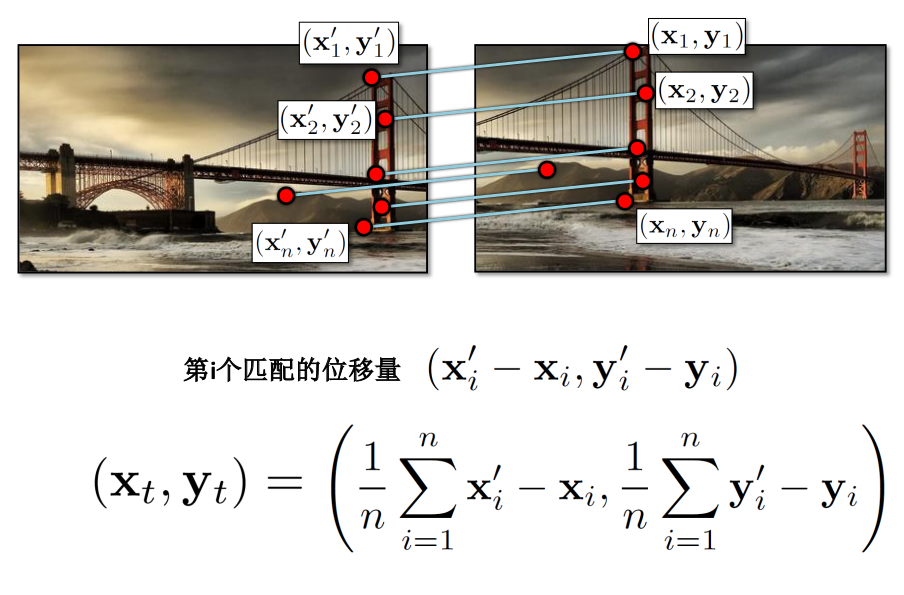
2019-10-31-15-50-10.png

我们可以通过两个图片位置坐标的差值直接获得位移量，但是这十分不恰当(因为图片总不是完全匹配的)

所以，就如图中所说，使用所有匹配点的差值的均值是一个很好的方法。

最小二乘法

对于仿射变换处理使用最小二乘法，这将很好的处理仿射变换，在平移问题，就相当于平均位移量。

从平移说起

对于一组平移图像，我们设其平移为$(X_t, Y_t)$

对于一个点$(X_i, Y_i)$， 我们有

\[X_i + X_t = X_i^{'}\\ Y_i + Y_t = Y_i^{'}\]

所以定义残差为

\[r_{xi}(X_t) = (X_i + X_t) - X'_i \\ r_{yi}(Y_t) = (Y_i + Y_t) - Y'_i\]

我们对于所有的匹配点求残差，这样，通过保证最小的残差平方和来求解$(X_t, Y_t)$

为了保证平移向量$(X_t, Y_t)$误差足够小，我们就需要保证他拥有最小的残差平方和:

\[C(X_t, Y_t) = \sum_{i=1}^{n}(r_{xi}(X_t)^2 + r_{yi}(Y_t)^2)\]

求解平移向量

对于这一过程，我们可以用矩阵表示

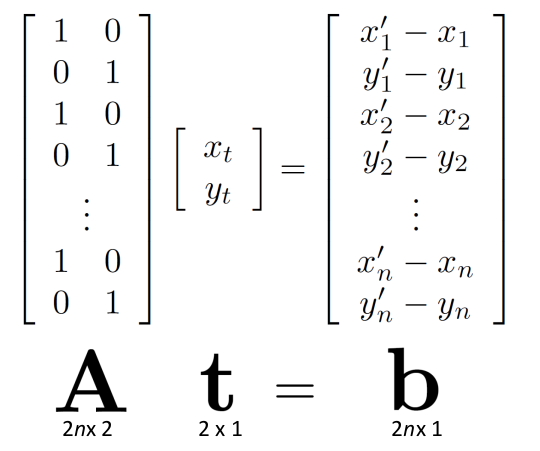
2019-10-31-16-27-59.png

为了保证最小的残差平方和则$\left |At - b \right |^{2}$要保证最小

为了求解t，我们就形成正则方程

\[A^TAt = A^Tb\\ t = (A^TA)^{-1}A^Tb\]

对于以上过程，需要注意的是，A是列满秩矩阵，否则，$A_{T}A$逆矩阵是不存在的。

当然对于非列满秩矩阵，我们还有其他方法。

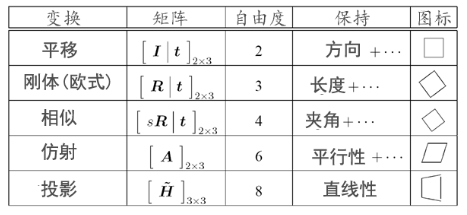
仿射变换

在图像的变换和卷绕时，我们就已经提到过仿射变换, emm，似乎讲的不大清楚。

具体的仿射变换矩阵是：

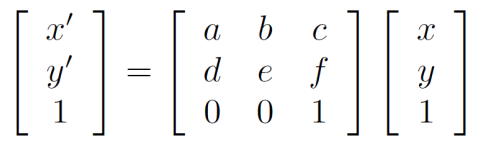
image-20191113150139165.png

为了求解仿射变换矩阵，我们同样使用最小二乘法来求解问题，定义残差和代价函数，并且将其转换为矩阵形式求解。

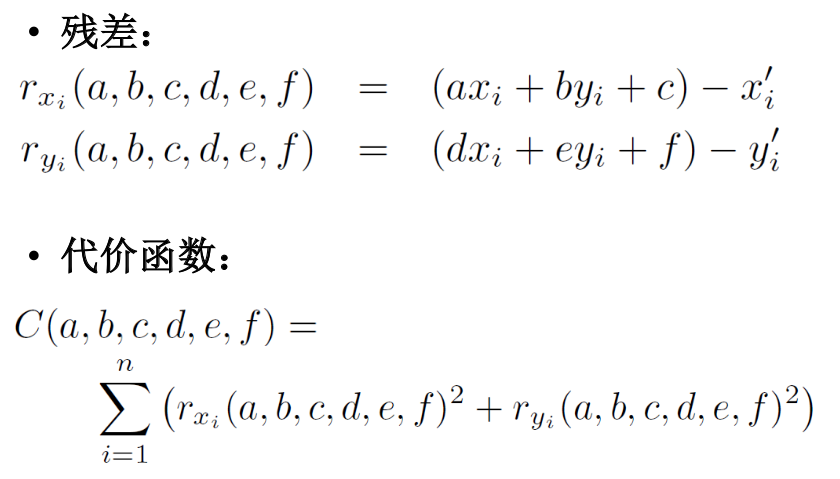
image-20191113150242406.png

image-20191113150253587.png

然后，我们就可以通过和平移一样的方法来求解t矩阵。

同态映射(Homographies)

同态映射的矩阵是：

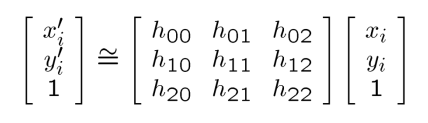
image-20191114221822655.png

我们按照正常的操作将其展开可以得到

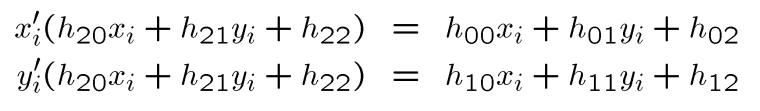
image-20191114221924111.png

由于上式是非线性的，所以我们将矩阵设为：

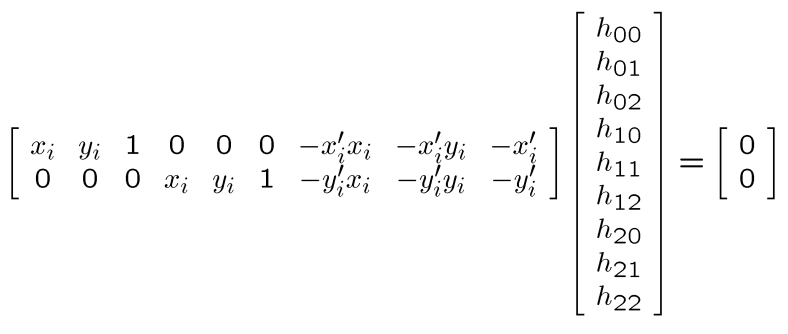
image-20191114223255851.png

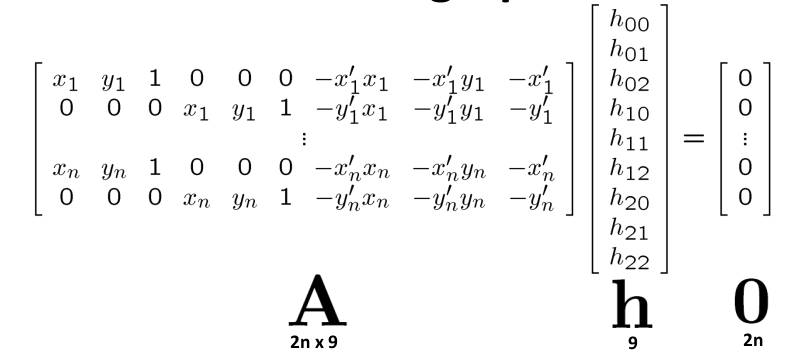
如果我们将这个参数扩展到xn,这时，我们就可以求解H矩阵了： image-20191114223341028.png

在上述的矩阵运算中即$Ah = 0$：

  • 因为h可缩放，因此限定问题的解$\hat{h}$为单位向量
  • $\hat{h}$是$A^TA$具有最小特征值的特征向量
  • 需要四个或更多匹配点

总结

通过上述的内容，我们明白了如何给两个图像配准对齐。

假定给定图像A和B，我们需要三个步骤

  1. 计算A和B的图像特征
  2. 匹配A和B之间的特征
  3. 使用匹配集计算A到B同态映射矩阵的最小二乘解

RANSAC(随机抽样一致)

在图像匹配的时候，我们就知道，可能存在匹配不正确的点，也就是离群点(outliers)

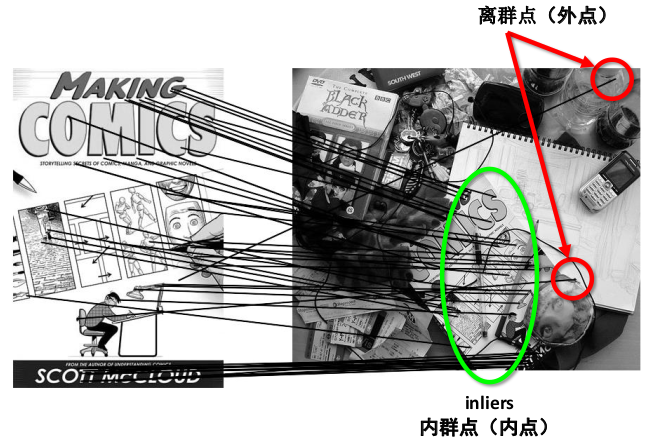
image-20191114230702540.png

而最小二乘法会去适应包括局外点在内的所有点，比如当我们在平移时求解$X_t$时，我们拟合曲线

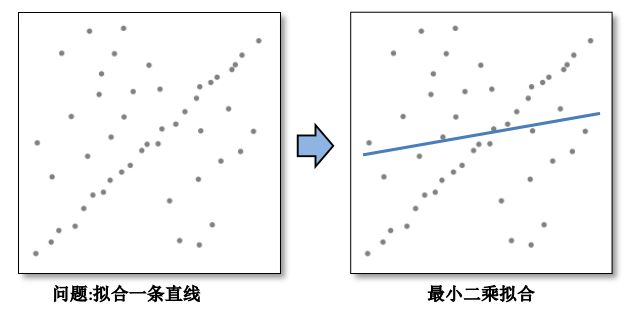
image-20191115100211114.png

可以看出，拟合的曲线是尽量适配所有点的，所以其结果不太准确。而RANSAC能得出一个仅仅用局内点计算出模型，并且概率还足够高。

RANSAC是“RANdom SAmple Consensus（随机抽样一致）”的缩写。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果；为了提高概率必须提高迭代次数。

RANSAC的基本过程是：

  1. 随机选择S个样本，同通常S是确定一个模型的最小样本数量。然后我们假设选取的样本全部是局内点。
  2. 使用S个样本计算模型的一个解。
  3. 用2求解出的一个模型计算其他所有数据，如果某个点适用于估计的模型，则认为是局内点。如果有足够多的局内点被归类为假设的局内点，则认为估计的模型足够合理
  4. 回到第一步，重复N次，并保留拥有最多局内点的模型。
  5. 然后重新使用所有的局内点去估计模型，因为它仅仅被初始的假设局内点估计过。

参数

从基本过程可以看出，RANSAC的正确率与局部点的比例和重复次数有关。我们设：

  • q为内点的概率
  • S为每次实验使用样本点的数目
  • P为最中成功找到正确解的概率
  • R为实验轮数

实验轮数

我们可以通过计算来确定实验的轮数R。通过上面的参数我们知道$q^{S}$是S个点均为局内点的概率，$1-q^{S}$是S个点中至少有一个点是局外点的概率，这说明这是一个不好的模型。所以$(1-q^{S})^{R}$表明算法永远不能选到正确解。

因此$1-P = (1-q^{S})^{R}$, 对两边求对数，我们就可以求得实验轮数值：

\[R = \frac{log(1-P)}{log(1-q^{S})}\]

通常情况下，我们并不知道P的值，但是我们可以给出一些鲁棒的值(难道是肉眼检测？？？)。

需要注意的是，这里假设n个点都是独立选择的，所以，当某个点被选定之后，它可能诶后续的迭代过程重新选定，这通常是不合理的，因此推导出的R值被看作是选取不重复点的上限。

为了得到更可信的参数，我们可以定义标准差被加到R上：

\[SD(R) = \frac{\sqrt{1-R^{S}}}{R^{S}}\]

实验采样数目

对于不同的变换，我们有不同的采样数目。

image-20191115110724025.png

优缺点

优点：

  • 简单，通用
  • 适用于许多不同的问题
  • 通常在实践中表现良好

缺点

  • 要調整参数
  • 有时需要太多的迭代
  • 极低局内点时可能失败
  • 同常可以比蛮力取样做的更好

Opencv实现

Opencv提供了calib3d模块，我们可以使用其中的cv.findhomography()用于找到两个图片的透视变换。

retval, mask = cv.findHomography(srcPoints, dstPoints, method, ransacReprojThreshold, mask, maxIters, confidence)

参数：

  • srcPoints: 原始平面中点的坐标，其类型为CV_32FC2的矩阵或vector 。很奇怪，为什么要双通道呢
  • dstPoints:目标平面中点的坐标，类型为CV_32FC2的矩阵或vector 。
  • method:用于计算单应矩阵的方法。可选参数：
    • 0： 常规方法，最小二乘法
    • RANSAC： 基于RANSAC的鲁棒方法
    • LMEDS: 最小中值稳健方法
    • RHO： 基于PROSAC的鲁棒方法
  • ransacReprojThreshold： 将点对视为内部值的最大允许重投影误差（仅在RANSAC和RHO方法中使用）。如果$| \texttt{dstPoints} _i - \texttt{convertPointsHomogeneous} ( \texttt{H} * \texttt{srcPoints} _i) |_2 > \texttt{ransacReprojThreshold} $那么就认为点i是局外点，如果rscPoints和dstPoints以像素为单位，则此参数应在1～10。
  • mask：通过可靠的方法（RANSAC或LMEDS）设置的可选输出掩码。请注意，输入掩码值将被忽略。
  • maxlters: RANSAC的最大迭代次数
  • confidence: 置信度， 介于0和1之间
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
orb = cv.ORB_create()

img1 = cv.imread('resources/yosemite/yosemite1.jpg')
gray1 = cv.cvtColor(img1, cv.COLOR_BGR2GRAY)
kp1, desc1 = orb.detectAndCompute(gray1, None)

img2 = cv.imread('resources/yosemite/yosemite2.jpg')
gray2 = cv.cvtColor(img2, cv.COLOR_BGR2GRAY)
kp2, desc2 = orb.detectAndCompute(gray2, None)

FLANN_INDEX_LSH = 6
index_params= dict(algorithm = FLANN_INDEX_LSH,
                   table_number = 6, # 12
                   key_size = 12,     # 20
                   multi_probe_level = 1) #2

search_params = dict(checks=50)   # or pass empty dictionary
flann = cv.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(desc1,desc2,k=2)

good = []
for m,n in matches:
    if m.distance < 0.7*n.distance:
        good.append(m)
        
src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1, 1, 2)# 双通道
dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1,1,2)

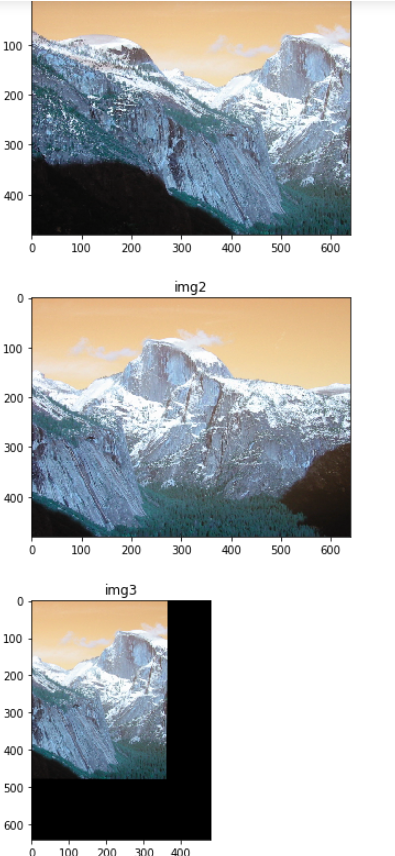
M, mask = cv.findHomography(src_pts, dst_pts, cv.RANSAC, 5.0)

plt.subplot(2, 2, 1)
plt.imshow(img1), plt.title('img1'), plt.show()
plt.subplot(2, 2, 2)
plt.imshow(img2), plt.title('img2'), plt.show()

img3 = cv.warpPerspective(img1, M, img1.shape[:2])
plt.subplot(2, 2, 3)
plt.imshow(img3), plt.title('img3'), plt.show()

image-20191115145900764.png

Toc
Related