Harris角点检测
理论
在图像中,角是各个方向强度变化很大的区域。
为了得到特征点,我们引入了局部窗口W。如果窗口W向任意方向的移动都导致图像灰度的明显变化,就意味着这是一个特征点。
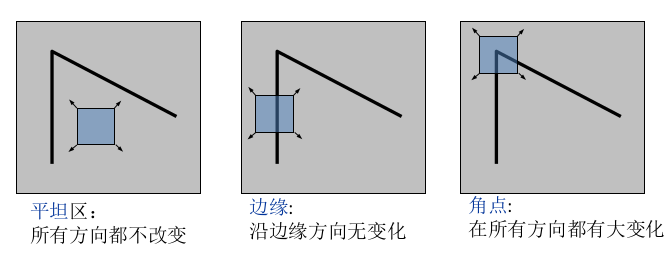
我们将窗口W平移(u, v), 那么我们可以得到窗口W内的所有像素的变化,也就是
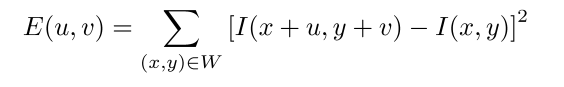
显然,E(u, v)越大,说明在(u, v)方向变化越大。
在图片中的移动可以简略为八个方向[(1, 0) (-1,0) (0, 1) (0,-1) (1, 1), (-1, -1)(1, -1) (-1, 1)](45度一个方向, 上下左右,加上两个对角线四个方向),然后我们可以得到得到八个方向上的E值,只要其中最小的E值仍然比较大,就意味着这是一个角度。
但是八个方向还是不够精确,我们通过泰勒公式(具体推倒见书)将上式展开就可以得到,一个更为简便的表示方式:
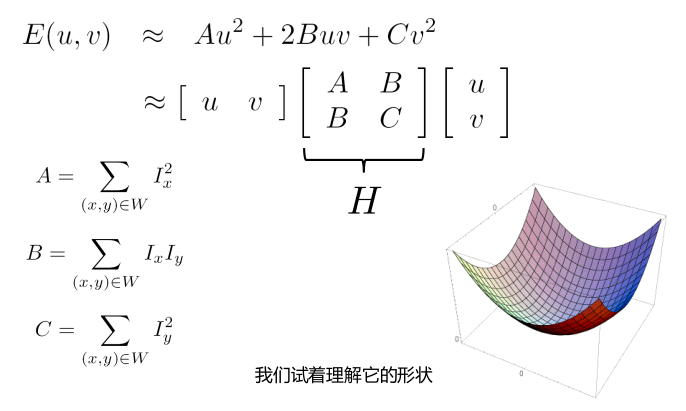
事实上,我们可以把E(u, v)的二次型函数想象成一个椭圆,其中两个轴的大小是矩阵H的两个特征值λ1和λ2。 而对应的x1和x2两个特征向量就是变化的方向(这个理论来自二次型矩阵,有空去看一下线性代数的二次型矩阵)。
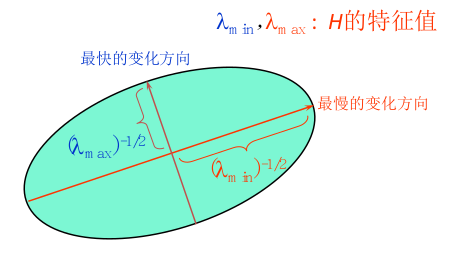
然后我们可以通过矩阵H得到特征值与对应的特征向量(线性代数好重要啊)。
不妨,现在有λmax和λmin两个特征值,Xmax和Xmin两个特征向量。如椭圆所示。
-
Xmax是E值增幅最快的方向, λmax是Xmax方向上增大的幅值
-
Xmin是E值增幅最小的方向, λmim是Xmin方向上增大的幅度 (也就是说在这个方向上,(u,v)的改变在使得E值变化不大)
(我一直无法理解,这到底是为什么,我仅阐述一下个人的看法)
大概是在Xmin方向,比如(0, 0)->(u,v)的一个变化,使得E值很小,这也就是像素的变化很小。
在前面已经给出,角点就是各个方向上都变化比较快的地方,所以,当λmin值也很大时,就说明该角点是各个方向上变化最快的地方。如图:

我们还有其他几种harris算子, 这比λmin更有效一些
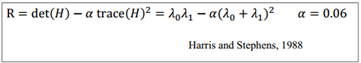

改进
由于存在噪声的原因,我们单纯的根据上式计算H矩阵效果不佳,将w窗口设置为一个高斯核,然后与H矩阵进行一次卷积。会得到更好的效果
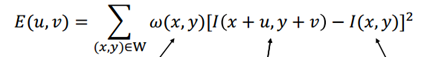
最后H矩阵就会成为变为
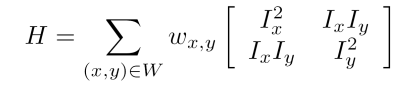
也就是说(实际上就是一个高斯卷积):
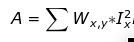
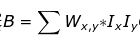
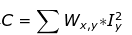
Harris角点特征不变性
特征不变形一般包括两个方面,不变性, 协变性, 一般不变性和协变性统称为不变性
不变性是指:图像变换后,角点位置不变
协变性是指: 如果两张同一图像的变换版本,则在相应的位置检测到相同特证
Harris角点的不变性
Harris角点检测对于平移变换和旋转变换和仿射强度是具有不变性的。
-
图像平移
首先,Harris角点检测由于是使用了一个窗口W进行检测, 所以哪怕图像平移了,对于特定的角点是不影响的
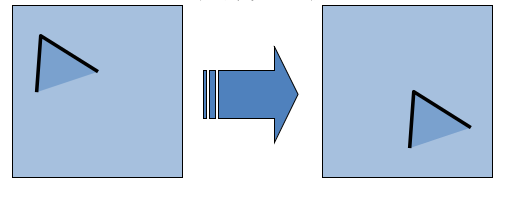
所以角点位置对平移变换是协变的
-
图像旋转
在计算Harris角点时,我们将计算公式等价为了一个椭圆,一个图像旋转了,但是某一个角点的椭圆跟着旋转但其特征值没有发生变化, (特征向量发生了变化)。
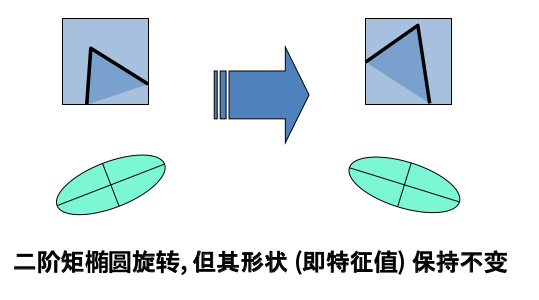
角点位置对旋转变换是协变的。
-
放射强度变换
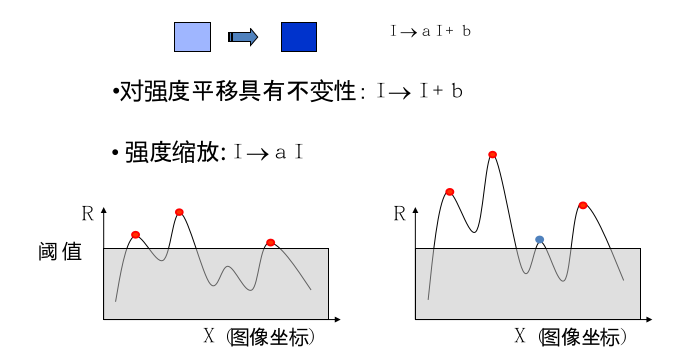
即使我们给一个图片增加了强度,但是由于我们在进行harris角点检测的时候使用的是微分运算,而微分运算对亮度的抬高和下降并不敏感。所以对亮度和对比度的仿射变换不改变harris相应的极值点出现的位置。但是会影响角点检测的数量。
-
尺度变换
Harris角点检测对于尺度变换不具有不变性, 如图
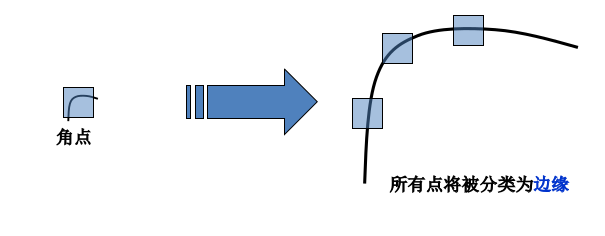
如果将一个角点放大,则会被检测为多个边缘而不是角点
为此,似乎有一个多尺度Harris角点检测,有空可以去看
实现步骤
- 先进行高斯滤波(可不做)
- 使用Sobel算子为每一个像素点求出Ix和Iy矩阵
- 为每一个像素点计算IxIx, IyIy, Ix*Iy。
- 为上一步中生成的三个矩阵进行高斯卷积, (需要注意的是,进行高斯卷积之后,矩阵中就已经存储的是A,B,C的值了。)
- 为每一个像素点生成矩阵H
- 然后选定特定的Harris算子求值, 并进行阈值处理 比如如果使用经典的Harris算子, 那么R=det(M)-αTrace(H)²=λ1λ2 - α(λ1+λ2)², 又因为特征值之积等于矩阵的行列式,特征值之和等于矩阵的对角线之和。所以R=AB-C² - α(A+B)²
- 寻找局部最大点。
Opencv实现
cv.cornerharris()是Opencv提供用于Harris角点检测的函数
Opencv提供的函数所使用的Harris算子是
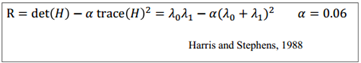
dst = cv.cornerHarris(src, blockSize, ksize, k, borderType)
参数:
- src: 原图像
- dst: 存储harris角点的R值,他的类型是CV_32FC1, 尺寸与图像相同。
- blockSize: 窗口大小
- ksize: Sobel算子的尺寸,一般为3
- k: alpha值, 一般为0.04~0.06
- borderType: 像素外推法
一般我们还会手动进行一次阈值处理来获得更为准确的角点(可选)