Wlgls 冲鸭!

第五节：计算机视觉--图像的变换和卷绕

2019-10-12
Computer_Vision

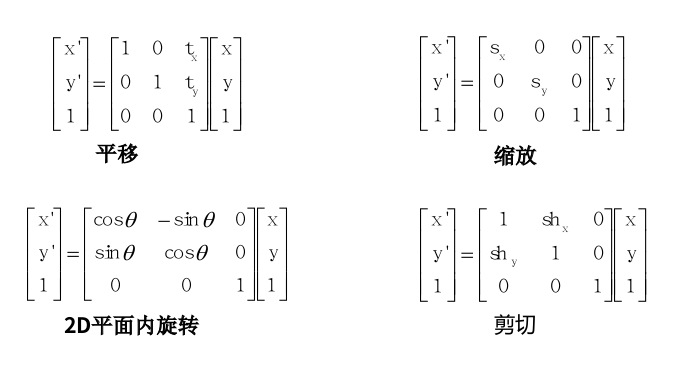
图像的变换和卷绕

图像的卷绕就相当与更改了图像的定义域

假设在某一点上f = g(x, y), 则经过了卷绕后，这一点f = g(h(x, y))

线性变化

首先了解一下线性变换，对于现行变换，我们可以使用2D矩阵来表示，比如对于某一点P,

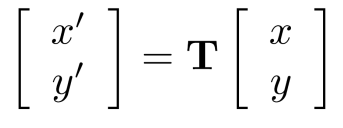
2019-10-12-17-17-07.png

等比缩放

等比缩放矩阵的是一个

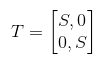
2019-10-17-15-00-08.png

所以 x’ = Sx; y’= Sy，

对于上面这一句话的函数， 我们假设变换后的图像为dst, 变换前的图像为src。则dst[x’, y’] = src[x, y]。

也许有一个问题，这样的变换，必然会缺少像素，所以使用相应的算法补全像素是必须的

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

def my_run(img):
    height, width = img.shape[:2]

    T = [[2, 0], [0, 2]]
    img2 = np.zeros((2*height, 2*width))

    for x in range(height):
        for y in range(width):
            p = np.dot(T, [[x], [y]])
            # print(p)
            x1, y1 = p
            x1 = x1[0]
            y1 = y1[0]
            # 扩大两倍，我就偷懒直接补好了
            img2[x1, y1] = img[x, y]
            img2[x1-1,y1-1] = img[x, y]
            img2[x1,y1-1] = img[x, y]
            img2[x1-1,y1] = img[x, y]

    return img2
if __name__ == '__main__':
    img = cv.imread('img/img.jpg', 0)
    img1 = my_run(img)
    cv.imwrite('img/img1.jpg', img1)
Opencv实现

cv2.resize()是Opencv提供用来进行等比缩进的函数

dst = cv.resize(src, dsize, dst, fx, fy, interpolation)

参数:

  • src: 原图像
  • dst: 输出图像
  • dsize: 输出图像尺寸，如果为0,则默认为(fxsrc.cols, fysrc.rows)
  • fx: 沿x轴的比例因子，为0时，由dsize决定
  • fy: 沿y轴的比例因子，为0时，由dsize决定
  • interpolation: 插值方法，缩小图像一般使用INTER_AREA， 放大图像时，一般使用INTER_CUBIC或者INTER_LINEAR 见官方文档

旋转

旋转矩阵是(以原点为中心)

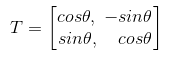
2019-10-17-15-05-05.png

如果具体计算一下，即x1 = cosθx-sinθy, y1 = sinθx+cosθy。

对于旋转变换，我们可以从一个像素点说起。

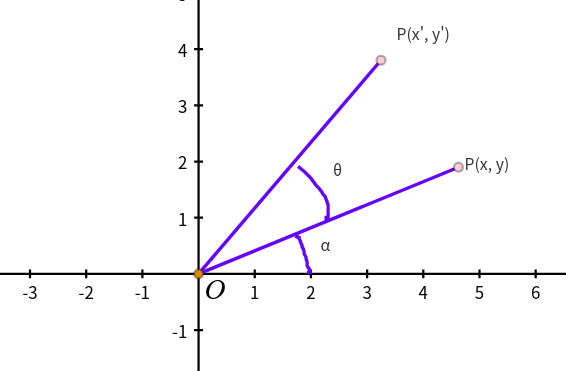
2019-10-17-15-28-09.png

对于一点P， 在图中如P(x, y)， 经过逆时针旋转θ

对于(x, y)有

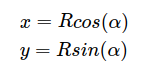
2019-10-17-15-42-44.png

但是对于旋转之后的图形，有

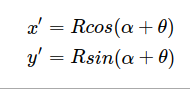
2019-10-17-15-42-25.png

将其分解，　就可以得到

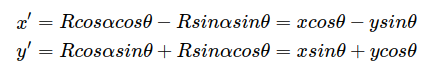
2019-10-17-15-47-01.png

Opencv实现

在Opencv中，实现为了得到这个特殊的矩阵，提供了cv.getRotationmatrix2D()这个函数。需要注意的是，这个函数返回的矩阵是2×3的矩阵，他可以规定旋转中心。

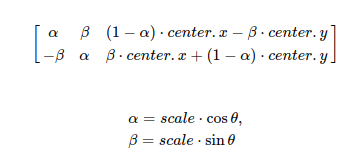
2019-10-12-20-33-54.png

retval = cv.getRotationmatrix2D(center, angle, scale)

参数：

  • retval: 返回的旋转矩阵, 2x3矩阵
  • center: 旋转的中心点
  • angle: 旋转的角度(正值表示逆时针旋转，原点在左上角))
  • scale: 各向同性的比例因子

总结

线性变换除了最常用的旋转和缩放，还有镜像

通常线性变换具有以下性质

  • 原点映射到原点
  • 直线映射到直线
  • 平行线保持平行
  • 比率被保持
  • 线性变换的组合仍是线性变换

平移

对于平移，假设有平移量为(tx, ty), 则(x1, x2) = (x+tx, y+ty)

单独的2×2的矩阵是无法实现平移操作的，我们需要一个2×3的矩阵，其基本样式为

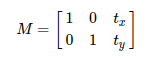
2019-10-13-10-31-46.png

其中tx和ty就代表着平移的量

但是一个2×3的矩阵和1×2的矩阵几乎无法运算得到(x+tx, y+ty)，所以我们扩展为齐次坐标，这个理由在后面。

仿射变换

了解仿射变换，我们先从了解齐次坐标开始。

齐次坐标

如果我们给(x, y)添加一个坐标，使其成为(x, y, w）， 这就是一个齐次坐标。

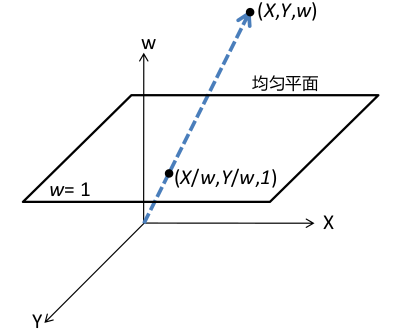
2019-10-13-11-21-58.png

我们从齐次坐标变为原坐标也十分简单，即(x, y, w)->(x/w, y/w)。

为了进行坐标的变换，则变换矩阵也变成了一个3×3的矩阵，比如平移矩阵变为了(可以自行计算以下，最后的变换格式就成了[x+tx, y+ty, 1])

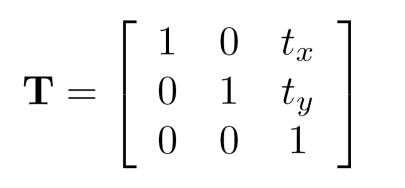
2019-10-13-11-24-38.png

所以，我们规定任何最后一行为[0 0 1]的3x3 矩阵表示的转换称为仿射变换。

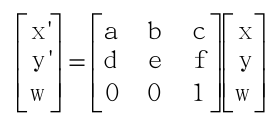
2019-11-13-15-28-54.png

之所以引入齐次坐标是为了更加便利的计算。仿射变换是由平移和线性变换组成的，而在前面提到平移矩阵是一个2×3的矩阵，而旋转矩阵是一个2×2的矩阵，这样子是无法进行组合的，所以，我们对其进行了扩展，也就产生了齐次坐标。

基本的仿射变换

2019-10-13-11-26-42.png

但是需要注意的是，在Opencv里实现，仍然要给cv.warpAffine()一个2×3的矩阵，而不是仿射矩阵,实际上，将仿射矩阵的最后一行抛弃就是2×3的矩阵了。

举例说明(旋转矩阵的由来)

一般的旋转矩阵T = [[cosθ, -sinθ], [sinθ, cosθ]]，是以原点为中心的旋转，但是在实际应用中，我们希望指定原点的位置。

为此Opencv提供了cv.getRotationMatrix2D()函数用于返回一个2×3的矩阵，规定中心点。这实际上就是平移和原始旋转的结合。

我们先将旋转中心移至中心，然后进行旋转，之后在进行平移即可。

性质

仿射变换是线性变换和平移的组合。

这样就可以说线性变换没有组合平移的仿射变换，平移是没有进行线性变换的仿射变换。

如图，大概就经历了旋转，平移，缩放三种变换的组合

2019-10-13-11-34-42.png

性质：

  • 原点不一定映射到原点
  • 直线映射到直线
  • 平行线保持平行
  • 保持比率
  • 仿射变换的组合是仿射变换

Opencv实现

由于得到仿射变换矩阵的算法过于麻烦，所以Opencv提供了一种更为简单的方式。

我们只需要原图像的三个点及其在输出图像中的对应位置，然后cv.getAffineTransform()就可以得到一个2×3的仿射矩阵。

之后使用cv.warpAffine()就可以得到变换

retval=cv.getAffineTransform(src, dst)

参数：

  • retval: 返回的2×3矩阵
  • src: 原图像的三个点的坐标
  • dst: 与原图像想对应的三个点的坐标

然后我们通过生成的这个函数就可以通过cv.warpAffine()进行仿射变换

dst = cv.warpAffine(src, M, dsize, dst, flages, borderMode, borderValue)

我们为cv.warpAffine()提供一个矩阵M， 当设置flags=cv.WARP_INVERSE_MAP时， 该函数就使用公式将其转换 即： dst(x,y)=src(M11x+M12y+M13,M21x+M22y+M23)， 也就是说是一个逆过程。如果没有设置，则需要提供正常进行的矩阵。

具体参阅文档官方

参数：

  • src: 原图像
  • M:2*3旋转矩阵
  • dsize： 输出图像的尺寸,其形式应为(width, height)
  • flags: 插值方法和可选标志WARP_INVERSE_MAP的组合，
  • borderMode：像素外推法，当borderMode=BORDER_TRANSPARENT时，表示目标图像中与原图像中的’离群值’相对应的像素未被函数修改
  • borderValue: 在边界不变的情况下使用的值；默认情况下为0。

我们通过旋转矩阵来进行实例说明

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

def rotation(img, flag = 0):
    height, width = img.shape[:2]
    # print(height, width)
    M = cv.getRotationMatrix2D(((width-1)/2.0, (height-1)/2.0), 90, 1)
    # print(M)
    if flag:
        dst = cv.warpAffine(img, M, (width, height), flags = cv.WARP_INVERSE_MAP)
    else:
        dst = cv.warpAffine(img, M, (width, height))
    # print(dst)
    return dst


if __name__ == '__main__':

    # img = cv.imread('img/img.jpg', -1)
    img = np.arange(200, 216).reshape(4, 4)
    img = img.astype(np.uint8)

    img1 = rotation(img)
    img2 = rotation(img, 1)
    # 设置flags

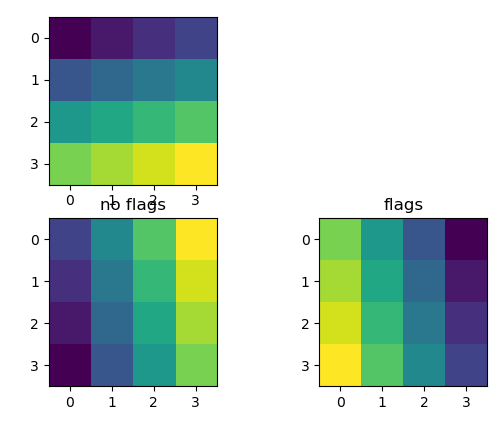
    plt.subplot(221)
    plt.imshow(img)

    plt.subplot(223)
    plt.imshow(img1)
    plt.title("no flags")

    plt.subplot(224)
    plt.imshow(img2)
    plt.title("flags")
    plt.show()

2019-11-13-15-20-31.png

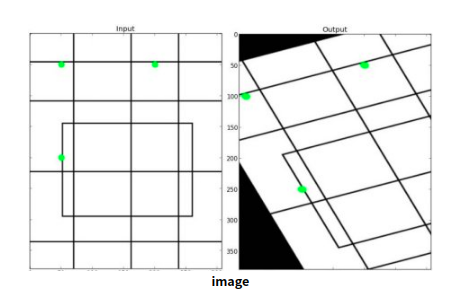
投影变换

投影变换又名透视变换、Homographies(同态映射，单应映射)

在最开始的图片，就是一个同态映射

其矩阵为：

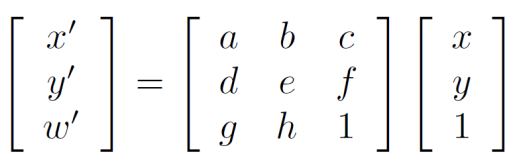
2019-11-13-15-43-13.png

同时他还有另外一种表示方式：

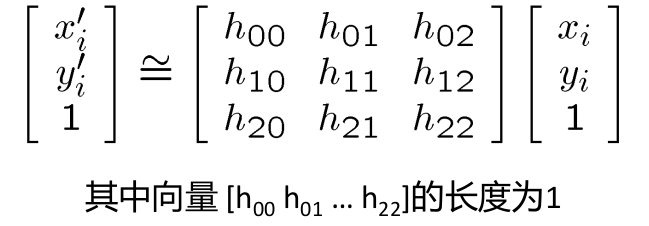
2019-11-13-15-43-39.png

即：

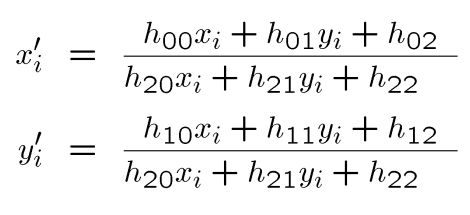
image-20191114222741081.png

性质：

  • 原点不一定映射到原点
  • 直线映射直线
  • 平行线不一定保持平行
  • 不保持比率
  • 投影变换的组合仍是投影变换

Opencv实现

Opencv提供了一个warpPerspective()函数用于处理单应映射。

dst = cv.warpPerspective(src, M, disize, dst, flags, borgerMode, borderValue)

参数：

  • src： 原图像
  • dst: 输出图像，其大小为dsize
  • M: 3*3投影矩阵
  • dsize: 输出头像的矩阵
  • flags: 差值方法和可选标志的组合，一般为WARP_INVERSE_MAP，此时，图像变换以上述理论计算。否则，应先使用invert反转转换。
  • borderMode： 像素外推法， 一般为BORDER_CONSTANT或BORDER_REPLICATE
  • borderValue: 在外界不变的情况下使用的值， 默认为0.
Toc
Related