在上一节,我们已经知道如何得到两个图像之间的转换关系,之后,我们就可以将两个图像进行拼装了。但是在了解图像的拼装之前,我们还需要了解一下图像形成的原理。
在现实世界中,物体是三维的,我们需要将一个三维的物体映射到一个二维的图像平面上。我们就必须了解一下相机的成像原理
图像形成
我们在此处只是讨论小孔成像,实际上透镜成像和小孔成像的基本相似。
我们知道,光线穿过小孔其传播方向是不发生改变的,所以,当现实世界的物体的光线透过小孔时,将产生一个反转的图像。
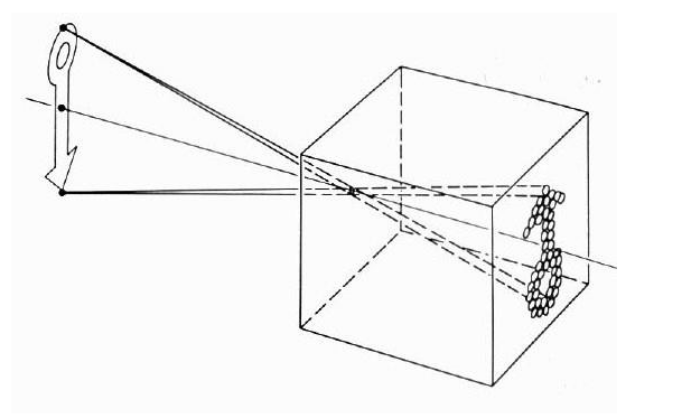
假如我们在小孔后方加一个成像平面,那么物体就会从一个三维变成一个二维图像。
从3D到2D
当三维物体的光线穿过小孔投影到投影平面PP时,我们需要将原本在相机坐标系上的点投影到像平面坐标系。我们假设三维世界有一个点,经过小孔后其坐标是为(x, y, z), 现在要将其投影到投影平面上。
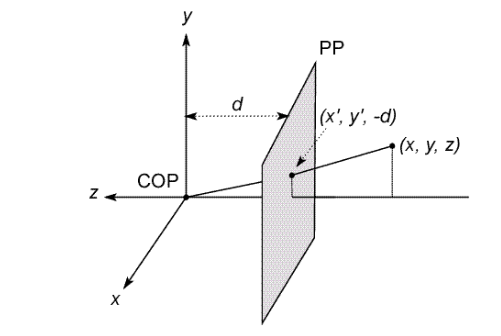
这个过程就是计算(x, y, z)到COP的直线与PP的交点,所以我们可以使用相似三角形。 并将Z坐标丢掉,就得到了成像平面上的点。其中原点在成像平面PP的中心。(z为负半轴) \((x, y, z) \rightarrow (-d{\frac{x}{z}}, -d{\frac{y}{z}},-d) \rightarrow (-d{\frac{x}{z}}, -d{\frac{y}{z}})\)
这不是一个线性变化,并不利于计算,所以,我们将其改为齐次坐标:

关于齐次坐标到原坐标的变换,我们只需要
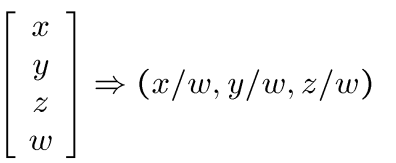
此时,我们就可以提供一个矩阵计算由3D齐次坐标变成2D齐次坐标了。
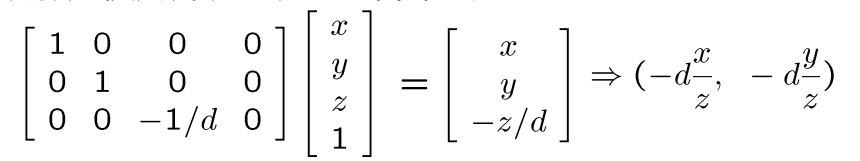
这就是透视投影,其中矩阵被称为投影矩阵,需要注意的是投影矩阵的尺度对变换无影响。
投影的性质
很明显,我当们将物体从3D降维到2D时,我们一定是失去了角度和距离。但是仍有一些属性保留了下来
-
多对一:同一光线上的所有点映射到图像中的同一点
-
点->点
-
线->线(保持共线性): 但是通过焦点的线变成一个点
-
平面->平面:但是通过焦点的平面变成一条线
-
平行线在消失点汇合:每个方向在空间都有他的消失点,但平行与图像平面的平行线保持平行

图像的坐标系
在成像过程中,我们一共需要四个坐标系,即
- 世界坐标系:即自然坐标系
- 相机坐标系: 以相机的关心为原点,Z轴指向相机前方,x轴向右,y轴向上
- 像平面坐标系: 即物体成像平面,通常是距光心一倍焦距的平面上, 原点在中心
- 像素平面坐标系: 像素平面坐标系的原点位于左上角,u轴向右与x轴平行,v轴向下与y轴平行。
在转换的过程中,我们是使用齐次坐标的
第一步: 将世界坐标系向相机坐标系转换
由于我们的相机坐标系和世界坐标系的原点不同,而我们在上述的转换过程中,(x, y, z)这一点的坐标是在相机坐标系下的,所以我们在进行3D到2D降维的过程就需要将世界坐标系向相机坐标系转换。
在转换的过程中,我们需要知道相机的位置和相机的方向(世界坐标系下)。例如,当前的世界坐标系和相机坐标系如图:
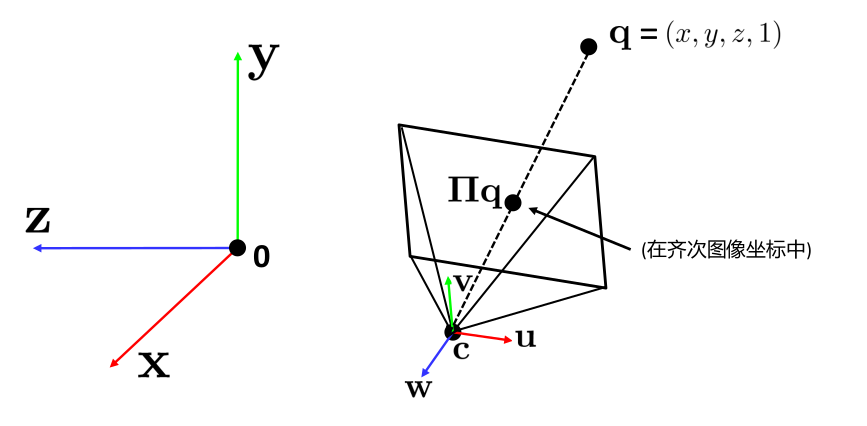
我们就需要进行平移和旋转两个步骤,只有这样才可以使相机坐标系为Z轴指向相机前方,X轴向右, Y轴向左。
首先进行平移,其平移矩阵为:
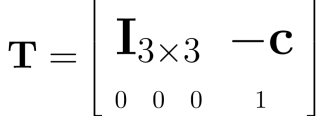
然后我们就将世界坐标系原点放在了相机坐标系原点了。
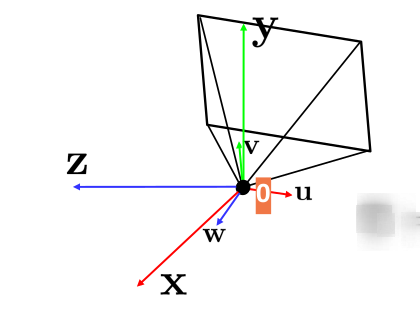
之后,我们在进行一次旋转即可将相机规范化.
其旋转矩阵为, 需要额外增加一行和一列[0 0 0 1]用来表示旋转矩阵:

此时相机坐标系和世界坐标系为:
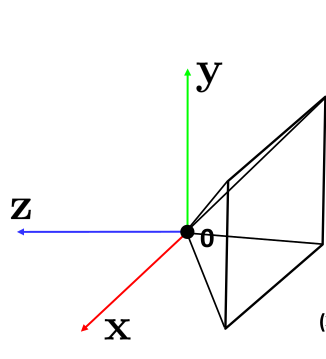
经过相机坐标系和世界坐标系的转换,我们就可以将3D的点映射到2D平面了。
第二步: 相机坐标系向平面坐标转换
我们首先在光心前做一个PP投影平面,将现实坐标系中的点投影到PP中

只是在此时我们将d置为1,也就是说此时的投影矩阵为:

即$[x/z, y/z, 1]^T = P * [X, Y, Z, 1]^T$
疑问:为什么此时的x,y坐标的正负与Z坐标有关?难道是投影到Z正半轴,然后投影回来吗,这样会保证最终获得的图片与现实坐标的是一致的。所以说也许PP投影面是在cop正半轴?
再之后,我们将这个PP平面映射到成像平面中,由于成像平面中的点与PP平面的点相连经过原点,仍然使用相似三角形就可以得到最终平面的位置:
第三步: 像面坐标系向像素坐标系的转换
-
我们知道在像素坐标系中,我们的原点在左上角, 而像面坐标系,其原点在中心,所以要进行转换,首先要将原点转到左上角。即:
\[\left\{\begin{matrix} u = x + c_{x} & \\ v = y + c_{y} & \end{matrix}\right.\] -
由于在计算机中,图片是由一个个像素组成的,其像素是矩形的,设其其长和宽分别时$\alpha$和$\beta$。设像素坐标为$(u, v, 1)^{T}$。所以我们的坐标转换为:
\[\left\{\begin{matrix} u =\alpha x + c_{x} & \\ v = \beta y + c_{y} & \end{matrix}\right.\] -
由于工艺的问题,我们甚至还存在倾斜因子s,这个实在无法理解,就先放放。
经此整合,我们就可以得到,从像面坐标系到像素坐标系的过程矩阵为:
\[\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} =\begin{bmatrix} \alpha & 0 & c_{x}\\ 0 & \beta & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]总结:
对与上述的三个步骤,我们完整的将一个3D物体投影到像素平面上。
经过总结,其矩阵为

我们将前两个合并就构成了相机的内参数(注意: 没有加入倾斜度)
\[\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} =\begin{bmatrix} -f\alpha & 0 & c_{x}\\ 0 & -f\beta & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 &0\\ 0 & 1 & 0 &0\\ 0 & 0 & 1 &0 \end{bmatrix}\begin{bmatrix}R_{3×3} & O_{3×1}\\O_{1×3}&1\end{bmatrix}\begin{bmatrix}I_{3×3} & T_{3×1}\\O_{1×3}&1\end{bmatrix}\begin{bmatrix} x\\ y\\ z \\ 1 \end{bmatrix}\]像素的内参数和外参数
在上述的过程中,其中K是内参数, 一般而阳,$\alpha, \beta$均为1
\[K =\begin{bmatrix} -f\alpha & 0 & c_{x}\\ 0 & -f\beta & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\]平移矩阵和旋转矩阵是外参数。
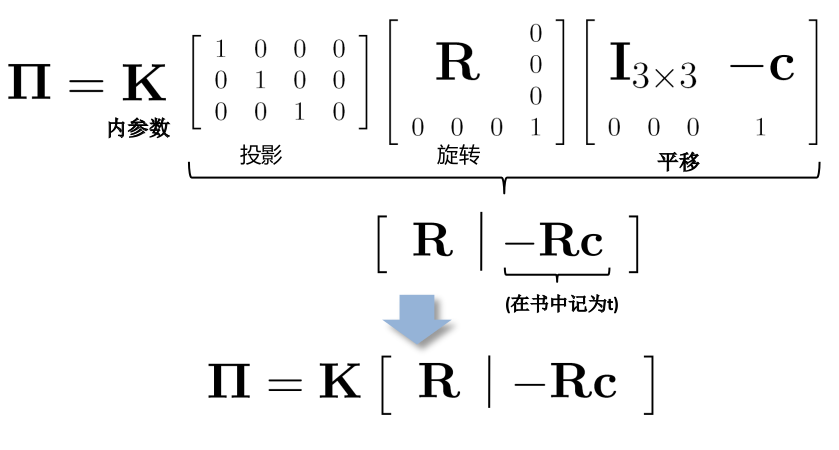
所以最后的投影矩阵就成了
失真
